今回は、神戸大学理系数学(2020年後期 第4問)の解説をしたいと思います。
問題
$i$ は虚数単位とし,$z=\cos\dfrac{\pi}{9}+i\sin\dfrac{\pi}{9}$ とする.また,複素数平面上の $5$ 点を $\mathrm{A}(0), \ $$\mathrm{B}(1), \ $$\mathrm{C}(z), \ $$\mathrm{D}(z^4), \ $$\mathrm{E}(z+z^5)$ によって定める.以下の問に答えよ.
⑴ $\triangle\mathrm{ACD}$ は正三角形となることを示せ.
⑵ $3$ 点 $\mathrm{B},\mathrm{C},\mathrm{E}$ は同一直線上にあることを示せ.
⑶ $\angle\mathrm{AED}$ の大きさを求めよ.
(神戸大学)
解答
⑴
$$\mathrm{AC}=|z|=1$$より
$$\mathrm{AD}=|z^4|=|z|^4=1$$である。
また、$z\ne 0$ より
$$\begin{align}
\angle\mathrm{CAD} &= \arg\dfrac{z^4-0}{z-0} \\
&= \arg z^3 \\
&= \arg\left(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\right) \\
&= \dfrac{\pi}{3}
\end{align}$$である。
以上より、$\triangle\mathrm{ACD}$ は $\mathrm{AC}=\mathrm{AD}=1, \ $$\angle\mathrm{CAD}=\dfrac{\pi}{3}$ の三角形、すなわち正三角形となる。$$\tag{証明終}$$
⑵
解法1(幾何)
$\mathrm{F}(z^5)$ とすると
$$\mathrm{AF}/\!/\mathrm{CE} \quad\cdots\text{①}$$である。
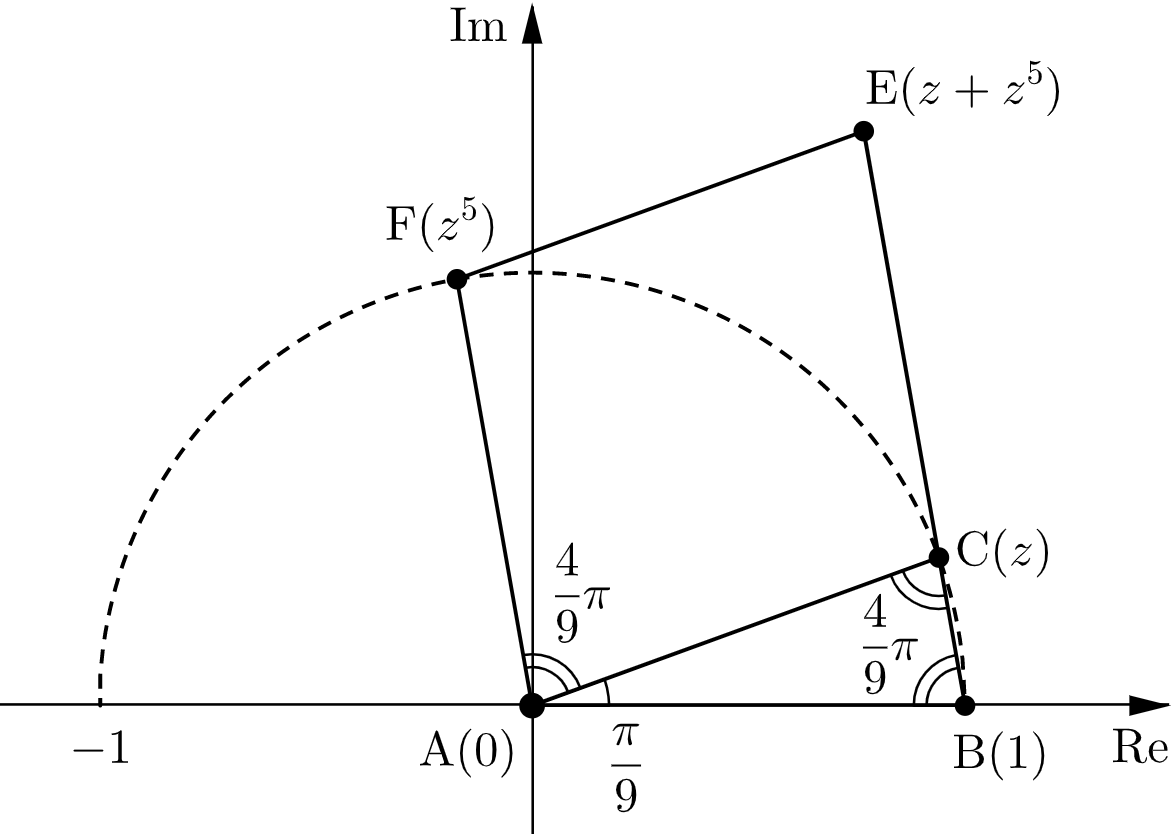
また
$$\begin{align}
\angle\mathrm{CAF} &= \angle\mathrm{BAF}-\angle\mathrm{BAC} \\
&= \dfrac{5}{9}\pi-\dfrac{\pi}{9} \\
&= \dfrac{4}{9}\pi
\end{align}$$である。
さらに、$\triangle\mathrm{ABC}$ は $\mathrm{AB}=\mathrm{BC}$ の二等辺三角形なので $\angle\mathrm{ABC}=\angle\mathrm{ACB}$ であるから
$$\begin{align}
\angle\mathrm{ACB} &= \dfrac{1}{2}\left(\pi-\dfrac{\pi}{9}\right) \\
&= \dfrac{4}{9}\pi
\end{align}$$となる。
したがって、$\angle\mathrm{CAF}=\angle\mathrm{ACB}$ となり、錯角の関係にある $2$ 角が等しいので
$$\mathrm{AF}/\!/\mathrm{BC} \quad\cdots\text{②}$$である。
①,②より
$$\mathrm{BC}/\!/\mathrm{CE}$$が成り立つので、$3$ 点 $\mathrm{B},\mathrm{C},\mathrm{E}$ は同一直線上にある。$$\tag{証明終}$$
解法2(計算)
$z\ne 1$ より
$$\begin{align}
\angle\mathrm{BCE} &= \arg\dfrac{z+z^5-z}{1-z} \\
&= \arg\dfrac{z^5}{1-z}
\end{align}$$である。
ここで
$$\begin{align}
\dfrac{z^5}{1-z} &= \dfrac{\cos\dfrac{5}{9}\pi+i\sin\dfrac{5}{9}\pi}{1-\cos\dfrac{\pi}{9}-i\sin\dfrac{\pi}{9}} \\
&= \dfrac{\left(\cos\dfrac{5}{9}\pi+i\sin\dfrac{5}{9}\pi\right)\left(1-\cos\dfrac{\pi}{9}+i\sin\dfrac{\pi}{9}\right)}{\left(1-\cos\dfrac{\pi}{9}-i\sin\dfrac{\pi}{9}\right)\left(1-\cos\dfrac{\pi}{9}+i\sin\dfrac{\pi}{9}\right)} \quad\cdots(*)
\end{align}$$であり
$$\begin{align}
((*)\text{の分子}) &= \cos\dfrac{5}{9}\pi-\cos\dfrac{5}{9}\pi\cos\dfrac{\pi}{9}-\sin\dfrac{5}{9}\pi\sin\dfrac{\pi}{9} \\
&\hphantom{=} \ +i\left(\sin\dfrac{5}{9}\pi-\sin\dfrac{5}{9}\pi\cos\dfrac{\pi}{9}+\cos\dfrac{5}{9}\pi\sin\dfrac{\pi}{9}\right) \\
&= \cos\dfrac{5}{9}\pi-\cos\left(\dfrac{5}{9}\pi-\dfrac{\pi}{9}\right) \\
&\hphantom{=} \ +i\left\{\sin\dfrac{5}{9}\pi-\sin\left(\dfrac{5}{9}\pi-\dfrac{\pi}{9}\right)\right\} \\
&= \cos\dfrac{5}{9}\pi-\cos\dfrac{4}{9}\pi+i\left(\sin\dfrac{5}{9}\pi-\sin\dfrac{4}{9}\pi\right) \\
&= -2\sin\dfrac{\pi}{2}\sin\dfrac{\pi}{18}+2\cos\dfrac{\pi}{2}\sin\dfrac{\pi}{18}i \\[0.3em]
&= -2\sin\dfrac{\pi}{18}
\end{align}$$$$\begin{align}
((*)\text{の分母}) &= 1-2\cos\dfrac{\pi}{9}+\cos^2\dfrac{\pi}{9}+\sin^2\dfrac{\pi}{9} \\
&= 2-2\cos\dfrac{\pi}{9} \\
&= 2-2\left(1-2\sin^2\dfrac{\pi}{18}\right) \\
&= 4\sin^2\dfrac{\pi}{18}
\end{align}$$より
$$\begin{align}
\angle\mathrm{BCE} &= \arg\dfrac{-2\sin\dfrac{\pi}{18}}{4\sin^2\dfrac{\pi}{18}} \\
&= \arg\left(-\dfrac{1}{2\sin\dfrac{\pi}{18}}\right) \\
&= \arg\left\{\dfrac{1}{2\sin\dfrac{\pi}{18}}(\cos\pi+i\sin\pi)\right\} \\
&= \pi
\end{align}$$となるから、$3$ 点 $\mathrm{B},\mathrm{C},\mathrm{E}$ は同一直線上にある。$$\tag{証明終}$$
⑶
⑴より、$\triangle\mathrm{ACD}$ は正三角形なので
$$\mathrm{CA}=\mathrm{CD}=1,\quad\angle\mathrm{ACD}=\dfrac{\pi}{3}$$である。
また
$$\mathrm{CE}=|z+z^5-z|=|z|^5=1$$より
$$\mathrm{CA}=\mathrm{CD}=\mathrm{CE} \quad\cdots\text{③}$$となる。
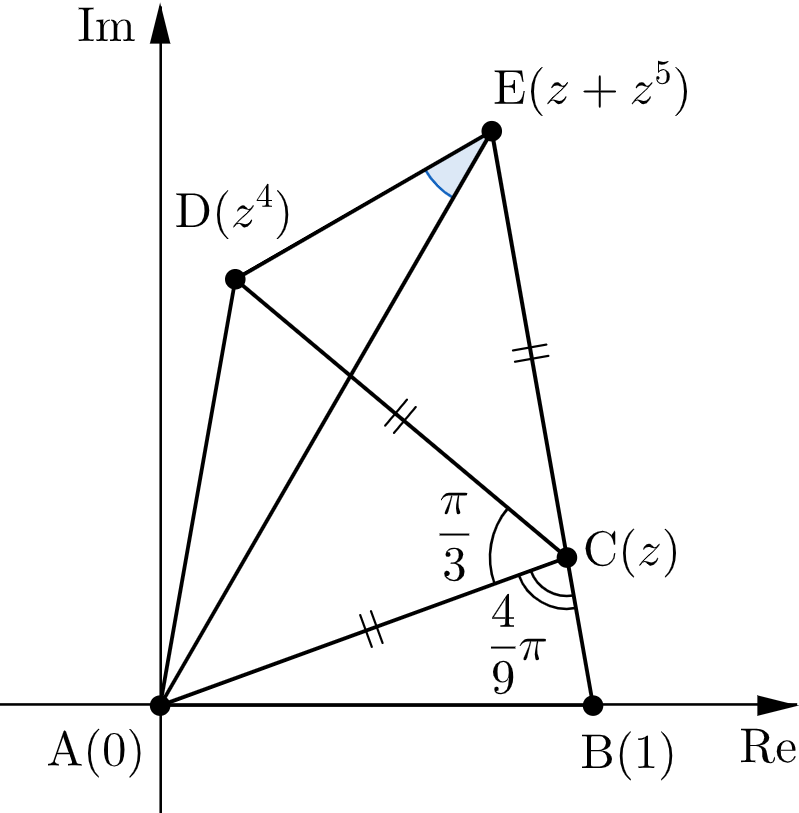
⑵より、$3$ 点 $\mathrm{B},\mathrm{C},\mathrm{E}$ は同一直線上にあるので
$$\begin{align}
\angle\mathrm{DCE} &= \pi-\dfrac{\pi}{3}-\dfrac{4}{9}\pi \\
&= \dfrac{2}{9}\pi
\end{align}$$となる。
③より、$\triangle\mathrm{CDE}$ は $\mathrm{CD}=\mathrm{CE}$ の二等辺三角形なので
$$\begin{align}
\angle\mathrm{CED} &= \dfrac{1}{2}\left(\pi-\dfrac{2}{9}\pi\right) \\
&= \dfrac{7}{18}\pi
\end{align}$$となる。
同様に、$\triangle\mathrm{CAE}$ は $\mathrm{CA}=\mathrm{CE}$ の二等辺三角形なので
$$\begin{align}
\angle\mathrm{CEA} &= \dfrac{1}{2}\left(\pi-\dfrac{\pi}{3}-\dfrac{2}{9}\pi\right) \\
&= \dfrac{2}{9}\pi
\end{align}$$となる。
したがって
$$\begin{align}
\angle\mathrm{AED} &= \angle\mathrm{CED}-\angle\mathrm{CEA} \\
&= \dfrac{7}{18}\pi-\dfrac{2}{9}\pi \\[0.3em]
&= \boldsymbol{\dfrac{\pi}{6}}
\end{align}$$
$$\boldsymbol{\dfrac{\pi}{6}}$$
解説
複素数の問題ですが、⑵で解法1を選択すれば幾何的な計算が中心となるため、そこまで複雑な計算は必要ありません。
⑶は、⑴,⑵をヒントとして解きますが、$\mathrm{CA}=\mathrm{CD}=\mathrm{CE}$ が意外と気づきにくい盲点かもしれません。
まとめ
今回は、神戸大学理系数学(2020年後期 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
神戸大学 理系数学 2020年[後期] 第1問 解説
神戸大学 理系数学 2020年[後期] 第2問 解説
神戸大学 理系数学 2020年[後期] 第3問 解説
神戸大学 理系数学 2020年[後期] 第4問 解説
神戸大学 理系数学 2020年[後期] 第5問 解説













