今回は、東京大学理系数学(2022年 第4問)の解説をしたいと思います。
問題
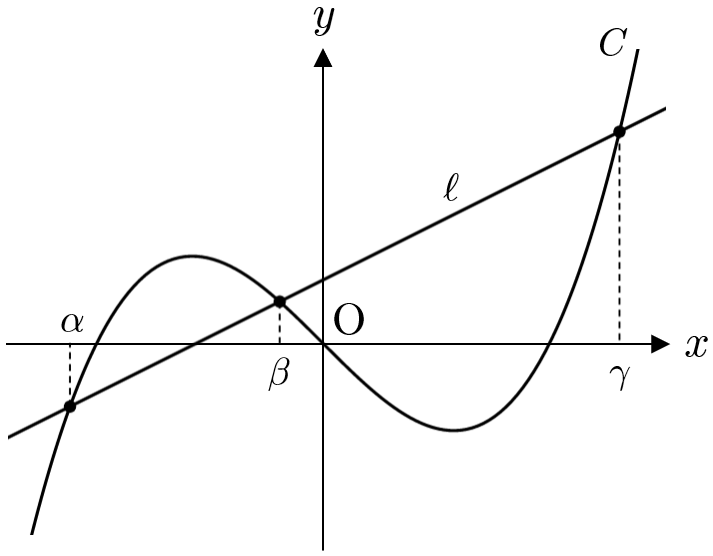
座標平面上の曲線$$C:\quad y=x^3-x$$を考える。
⑴ 座標平面上のすべての点 $\mathrm{P}$ が次の条件(ⅰ)を満たすことを示せ。
(ⅰ) 点 $\mathrm{P}$ を通る直線 $\ell$ で,曲線 $C$ と相異なる $3$ 点で交わるものが存在する。⑵ 次の条件(ⅱ)を満たす点 $\mathrm{P}$ のとりうる範囲を座標平面上に図示せよ。
(東京大学)
(ⅱ) 点 $\mathrm{P}$ を通る直線 $\ell$ で,曲線 $C$ と相異なる $3$ 点で交わり,かつ,直線 $\ell$ と曲線 $C$ で囲まれた $2$ つの部分の面積が等しくなるものが存在する。
解答
⑴
$\mathrm{P}$ の座標を $(a,b)$ とおく。
$\ell$ が $y$ 軸に平行なとき、$\ell$ と $C$ が相異なる $3$ 点で交わることはないので、$\ell$ は $y$ 軸に平行ではない。
よって、$\ell$ の傾きを $k$ とおくと、$\ell$ の方程式は
$$y=k(x-a)+b$$となる。これと $C$ の方程式から $y$ を消去すると
$$\begin{array}{c}
x^3-x=k(x-a)+b \\
\therefore\quad x^3-(k+1)x+ak-b=0\quad\cdots\text{①}
\end{array}$$
①の解は $\ell$ と $C$ の共有点の $x$ 座標を表すので、①が相異なる $3$ つの実数解をもてば条件(ⅰ)がみたされる。
①の左辺を $f(x)$ とおくと
$$f'(x)=3x^2-(k+1)$$
$k\leqq -1$ のとき $f'(x)\geqq 0$ なので $f(x)$ は単調増加であり、①が相異なる $3$ つの実数解をもつことはない。
$k\gt -1$ のとき
$$f'(x)=3\left(x+\sqrt{\dfrac{k+1}{3}}\right)\left(x-\sqrt{\dfrac{k+1}{3}}\right)$$より、増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c}\hline
x & \cdots & -\sqrt{\dfrac{k+1}{3}} & \cdots & \sqrt{\dfrac{k+1}{3}} & \cdots \\ \hline
f’(x) & + & 0 & – & 0 & + \\ \hline
f(x) & \nearrow & \text{極大} & \searrow & \text{極小} & \nearrow \\ \hline
\end{array}$$
また、$\displaystyle\lim_{x\to\pm\infty}f(x)=\pm\infty$(複号同順)より、極大値と極小値が異符号、すなわちこれらの積が負となればよい。
$$\begin{array}{c}
f\left(-\sqrt{\dfrac{k+1}{3}}\right)f\left(\sqrt{\dfrac{k+1}{3}}\right)\lt 0 \\
\left\{2\left(\dfrac{k+1}{3}\right)^\frac{3}{2}+ak-b\right\}\left\{-2\left(\dfrac{k+1}{3}\right)^\frac{3}{2}+ak-b\right\}\lt 0 \\
(ak-b)^2-\dfrac{4}{27}(k+1)^3\lt 0\quad\cdots\text{②}
\end{array}$$
②の左辺は $k$ の $3$ 次式かつ最高次の係数が負なので、十分大きい実数 $k$ をとることで②は成り立つ。すなわち、任意の実数 $a,b$ に対して、①が相異なる $3$ つの実数解をもつような実数 $k$ が存在する。
したがって、座標平面上のすべての点 $\mathrm{P}$ が条件(ⅰ)をみたす。$$\tag{証明終}$$
⑵
⑴より、座標平面上のすべての点 $\mathrm{P}$ が条件(ⅰ)をみたすので、$\ell$ と $C$ の交点の $x$ 座標を $\alpha,\beta,\gamma$( $\alpha\lt\beta\lt\gamma$ )とおく。
このとき
$$f(x)=(x-\alpha)(x-\beta)(x-\gamma)\quad\cdots\text{③}$$と因数分解できる。
$\ell$ と $C$ で囲まれた $2$ つの部分の面積が等しいという条件より
$$\begin{eqnarray}
\displaystyle\int_\alpha^\beta \left[\left(x^3-x\right)-\{k(x-a)+b\}\right]dx &=& \displaystyle\int_\beta^\gamma \left[\{k(x-a)+b\}-\left(x^3-x\right)\right]dx \\
\displaystyle\int_\alpha^\beta f(x)dx + \displaystyle\int_\beta^\gamma f(x)dx &=& 0 \\
\displaystyle\int_\alpha^\gamma f(x)dx &=& 0 \\
\displaystyle\int_\alpha^\gamma (x-\alpha)(x-\beta)(x-\gamma)dx &=& 0 \quad\text{(}\because\text{③)}
\end{eqnarray}$$
③の左辺に対して部分積分を行うと
$$\begin{eqnarray}
0 &=& \displaystyle\int_\alpha^\gamma (x-\alpha)(x-\beta)(x-\gamma)dx \\
&=& \displaystyle\int_\alpha^\gamma (x-\alpha)\{(x-\alpha)+(\alpha-\beta)\}(x-\gamma)dx \\
&=& \displaystyle\int_\alpha^\gamma (x-\alpha)^2(x-\gamma)dx
+ (\alpha-\beta)\displaystyle\int_\alpha^\gamma (x-\alpha)(x-\gamma)dx \\
&=& \left[\dfrac{1}{3}(x-\alpha)^3(x-\gamma)-\dfrac{1}{12}(x-\alpha)^4\right]_\alpha^\gamma
+ (\alpha-\beta)\left[\dfrac{1}{2}(x-\alpha)^2(x-\gamma)-\dfrac{1}{6}(x-\alpha)^3\right]_\alpha^\gamma \\
&=& -\dfrac{1}{12}(\gamma-\alpha)^4 -\dfrac{1}{6}(\alpha-\beta)(\gamma-\alpha)^3 \\
&=& -\dfrac{1}{12}(\gamma-\alpha)^3(\alpha+\gamma-2\beta)
\end{eqnarray}$$
$\gamma-\alpha \ne 0$ より
$$\alpha+\gamma-2\beta=0\quad\cdots\text{④}$$
また、$f(x)$ の $2$ 次の係数は $0$ なので、解と係数の関係より
$$\alpha+\beta+\gamma=0\quad\cdots\text{⑤}$$
④,⑤より $\beta=0$ であり、このとき $\ell$ と $C$ は原点を含む相異なる $3$ 点で交わる。
したがって、$\ell$ は原点を通るので $ak-b=0\quad\cdots\text{⑥}$ となる。
⑴より、$\ell$ と $C$ が相異なる $3$ 点で交わるための条件は $k\gt -1$ かつ②であるが、⑥のとき、$k\gt -1$ なるすべての実数 $k$ で②は成り立つ。
よって、条件(ⅱ)をみたす点 $\mathrm{P}$ が存在するための条件は「⑥かつ $k\gt -1$ 」をみたす実数 $k$ が存在することである。
(ア) $a=0$ のとき
⑥より $b=0$ であり、このとき $k\gt -1$ をみたす実数 $k$ は存在する。
(イ) $a\ne 0$ のとき
⑥より $k=\dfrac{b}{a}$ であり、$k\gt -1$ より $\dfrac{b}{a}\gt -1$ である。
すなわち
$$\begin{cases}
b\gt -a & \text{(} \ a\gt 0 \ \text{のとき)} \\
b\lt -a & \text{(} \ a\lt 0 \ \text{のとき)}
\end{cases}$$
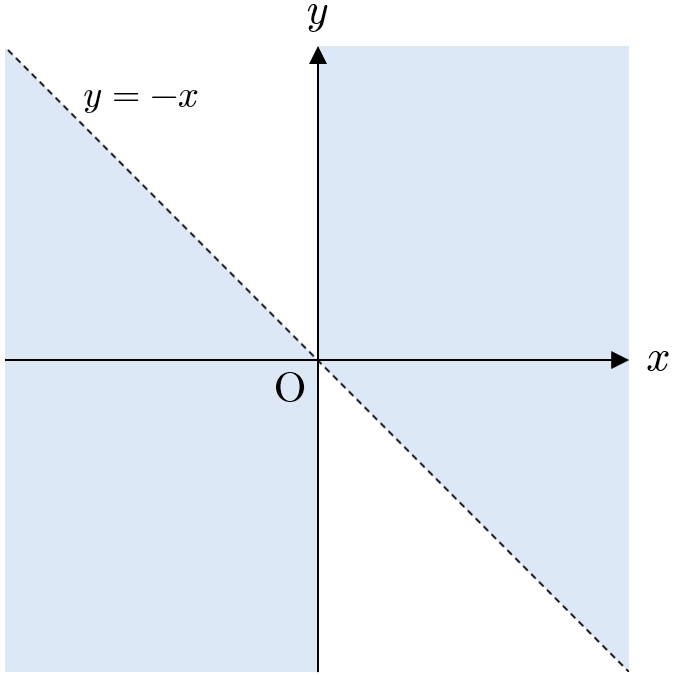
(ア),(イ)より、条件(ⅱ)をみたす点 $\mathrm{P}$ のとりうる範囲は、下図の網掛け部分である。ただし、境界は原点のみ含む。
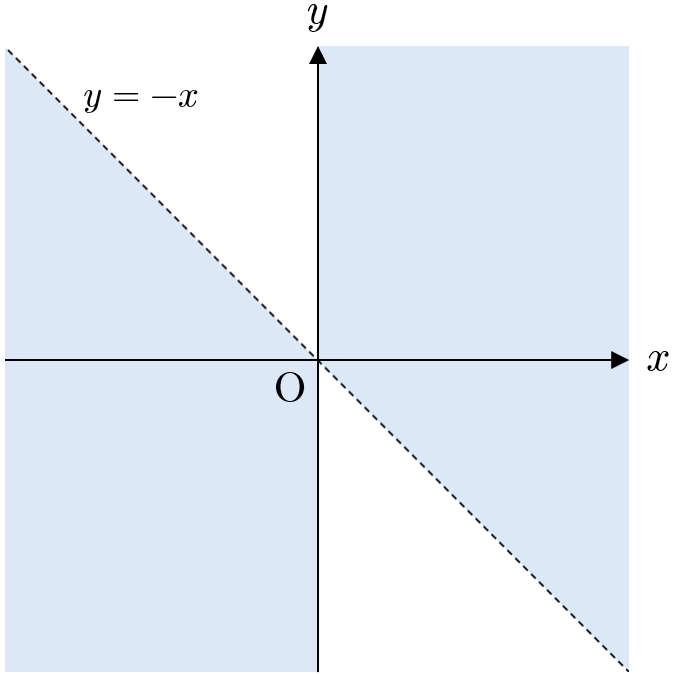
下図の網掛け部分(境界は原点のみ含む)
解説
この問題は「状況を図的にイメージできる力」「式を用いて論理的に説明する力」の両方が求められる問題となっており、得意な人と苦手な人に分かれそうな良問だと思います。
⑴は座標平面上のどの点を与えられても、その点を通るように「傾きのとても大きい直線」を引けば、必ず $C$ と相異なる $3$ 点で交わる、ということを式を用いて説明しています。
$3$ 次方程式 $f(x)=0$ が異なる $3$ つの実数解をもつとき、$f(x)$ は $2$ つの極値をもち、それらの積が負になる、というのは練習問題などで経験しておきたい内容です。
⑵は、$2$ つの面積が等しいとき、必ず $\ell$ は原点を通るということを示すのが山場だと思います。本解答のように部分積分を行うことで計算量・計算ミスを減らしましょう。
まとめ
今回は、東京大学理系数学(2022年 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2022年 第1問 解説
東京大学 理系数学 2022年 第2問 解説
東京大学 理系数学 2022年 第3問 解説
東京大学 理系数学 2022年 第4問 解説
東京大学 理系数学 2022年 第5問 解説
東京大学 理系数学 2022年 第6問 解説













