今回は、神戸大学理系数学(2019年 第2問)の解説をしたいと思います。
問題
$|\overrightarrow{\mathrm{AB}}|=2$ をみたす $\triangle\mathrm{PAB}$ を考え,辺 $\mathrm{AB}$ の中点を $\mathrm{M}$,$\triangle\mathrm{PAB}$ の重心を $\mathrm{G}$ とする.以下の問に答えよ.
⑴ $|\overrightarrow{\mathrm{PM}}|^2$ を内積 $\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}$ を用いて表せ.
⑵ $\angle\mathrm{AGB}=\dfrac{\pi}{2}$ のとき,$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}$ の値を求めよ.
⑶ 点 $\mathrm{A}$ と 点 $\mathrm{B}$ を固定し,$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}=\dfrac{5}{4}$ をみたすように点 $\mathrm{P}$ を動かすとき,$\angle\mathrm{ABG}$ の最大値を求めよ.ただし,$0\lt\angle\mathrm{ABG}\lt\pi$ とする.
(神戸大学)
解答
⑴
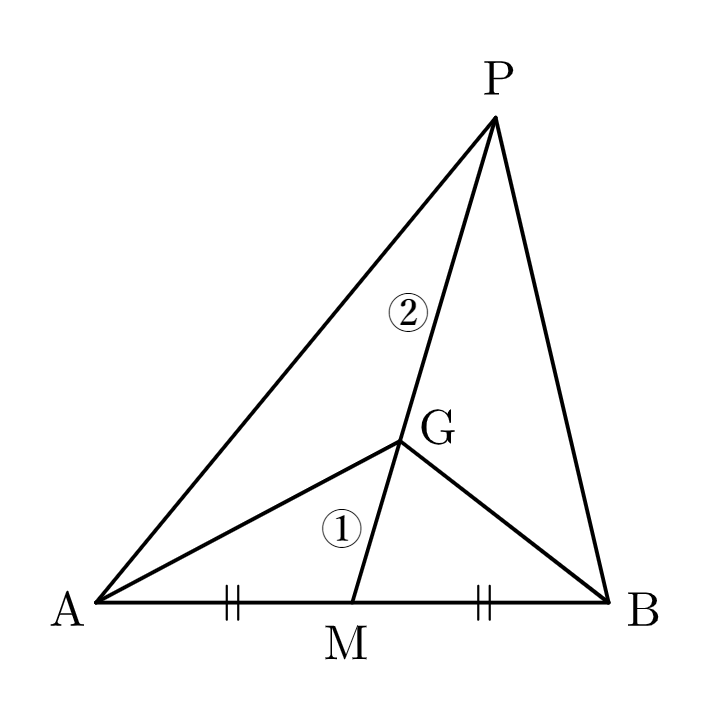
$\triangle\mathrm{PAB}$ において、余弦定理により
$$\begin{array}{c}
\begin{aligned}
|\overrightarrow{\mathrm{AB}}|^2 &= |\overrightarrow{\mathrm{PA}}|^2+|\overrightarrow{\mathrm{PB}}|^2-2|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PB}}|\cos\angle\mathrm{APB} \\
4 &= |\overrightarrow{\mathrm{PA}}|^2+|\overrightarrow{\mathrm{PB}}|^2-2|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PB}}|\dfrac{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}}{|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PB}}|}
\end{aligned} \\[0.3em]
\therefore \ |\overrightarrow{\mathrm{PA}}|^2+|\overrightarrow{\mathrm{PB}}|^2=4+2\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}} \quad\cdots\text{①}
\end{array}$$
点 $\mathrm{M}$ は辺 $\mathrm{AB}$ の中点なので
$$\begin{align}
|\overrightarrow{\mathrm{PM}}|^2 &= \left|\dfrac{1}{2}(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}})\right|^2 \\
&=\dfrac{1}{4}(|\overrightarrow{\mathrm{PA}}|^2+|\overrightarrow{\mathrm{PB}}|^2+2\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}) \\
&= \dfrac{1}{4}(4+2\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}+2\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}) \ \text{(}\because\text{①)} \\
&= \boldsymbol{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}+1}
\end{align}$$
$$\boldsymbol{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}+1}$$
⑵
$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}=x$ とおく。
ここで
$$\begin{align}
\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PM}} &= \overrightarrow{\mathrm{PA}}\cdot\dfrac{1}{2}(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}}) \\
&= \dfrac{1}{2}|\overrightarrow{\mathrm{PA}}|^2+\dfrac{1}{2}x, \\[0.5em]
\overrightarrow{\mathrm{PB}}\cdot\overrightarrow{\mathrm{PM}} &= \overrightarrow{\mathrm{PB}}\cdot\dfrac{1}{2}(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}}) \\
&= \dfrac{1}{2}|\overrightarrow{\mathrm{PB}}|^2+\dfrac{1}{2}x
\end{align}$$より
$$\begin{align}
\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{PB}}\cdot\overrightarrow{\mathrm{PM}} &= \dfrac{1}{2}(|\overrightarrow{\mathrm{PA}}|^2+|\overrightarrow{\mathrm{PB}}|^2)+x \\
&= \dfrac{1}{2}(4+2x)+x \ \text{(}\because\text{①)} \\
\therefore \ \overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{PB}}\cdot\overrightarrow{\mathrm{PM}} &= 2+2x \quad\cdots\text{②}
\end{align}$$である。
したがって、$\angle\mathrm{AGB}=\dfrac{\pi}{2}$ より
$$\begin{align}
0 &= \overrightarrow{\mathrm{GA}}\cdot\overrightarrow{\mathrm{GB}} \\
&= (\overrightarrow{\mathrm{GP}}+\overrightarrow{\mathrm{PA}})\cdot(\overrightarrow{\mathrm{GP}}+\overrightarrow{\mathrm{PB}}) \\
&= \left(\overrightarrow{\mathrm{PA}}-\dfrac{2}{3}\overrightarrow{\mathrm{PM}}\right)\cdot\left(\overrightarrow{\mathrm{PB}}-\dfrac{2}{3}\overrightarrow{\mathrm{PM}}\right) \\
&= x-\dfrac{2}{3}(\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{PB}}\cdot\overrightarrow{\mathrm{PM}})+\dfrac{4}{9}|\overrightarrow{\mathrm{PM}}|^2 \\
&= x-\dfrac{2}{3}(2+2x)+\dfrac{4}{9}(x+1) \ \text{(}\because\text{②,⑴)} \\
&= \dfrac{1}{9}x-\dfrac{8}{9}
\end{align}$$となるので
$$x=\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}=\mathbf{8}$$
$$\mathbf{8}$$
⑶
⑵より
$$\overrightarrow{\mathrm{GA}}\cdot\overrightarrow{\mathrm{GB}}=\dfrac{1}{9}\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}-\dfrac{8}{9}$$であり、条件より $\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}=\dfrac{5}{4}$ であるから
$$\overrightarrow{\mathrm{GA}}\cdot\overrightarrow{\mathrm{GB}}=\dfrac{1}{9}\cdot\dfrac{5}{4}-\dfrac{8}{9}=-\dfrac{3}{4}$$となる。
よって
$$\begin{align}
\cos\angle\mathrm{ABG} &= \dfrac{\overrightarrow{\mathrm{BA}}\cdot\overrightarrow{\mathrm{BG}}}{|\overrightarrow{\mathrm{BA}}||\overrightarrow{\mathrm{BG}}|}=\dfrac{\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{GB}}}{2|\overrightarrow{\mathrm{GB}}|} \\
&= \dfrac{(\overrightarrow{\mathrm{GB}}-\overrightarrow{\mathrm{GA}})\cdot\overrightarrow{\mathrm{GB}}}{2|\overrightarrow{\mathrm{GB}}|} \\
&= \dfrac{|\overrightarrow{\mathrm{GB}}|^2+\dfrac{3}{4}}{2|\overrightarrow{\mathrm{GB}}|} \\
&= \dfrac{1}{2}|\overrightarrow{\mathrm{GB}}|+\dfrac{3}{8|\overrightarrow{\mathrm{GB}}|}
\end{align}$$となる。
$|\overrightarrow{\mathrm{GB}}|\gt 0$ より、相加・相乗平均の大小関係から
$$\cos\angle\mathrm{ABG}\geqq 2\sqrt{\dfrac{1}{2}|\overrightarrow{\mathrm{GB}}|\cdot\dfrac{3}{8|\overrightarrow{\mathrm{GB}}|}}=\dfrac{\sqrt{3}}{2}$$が成り立つ。等号成立は $\dfrac{1}{2}|\overrightarrow{\mathrm{GB}}|=\dfrac{3}{8|\overrightarrow{\mathrm{GB}}|}$ すなわち $|\overrightarrow{\mathrm{GB}}|=\dfrac{\sqrt{3}}{2}$ のときである。
したがって
$$0\lt\angle\mathrm{ABG}\leqq\dfrac{\pi}{6}$$となるので、$\angle\mathrm{ABG}$ の最大値は $\boldsymbol{\dfrac{\pi}{6}}$ である。
$$\boldsymbol{\dfrac{\pi}{6}}$$
解説
$1$ 辺のみ長さが分かっている三角形に関するベクトルの問題で、⑶がやや難しいです。
⑴は、$\mathrm{M}$ が辺 $\mathrm{AB}$ の中点ということから立式していきます。
⑵は、垂直条件が与えられているので、$\overrightarrow{\mathrm{GA}}\cdot\overrightarrow{\mathrm{GB}}=0$ から始めれば、答えまでたどり着けると思います。
⑶は、ぱっと見⑴,⑵との関連性が低そうに見えるので、難しいと思います。
⑵でつくった式に $\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}=\dfrac{5}{4}$ を代入すると、$\triangle\mathrm{GAB}$ の中だけで考えることができます。
$0\lt\theta\lt\pi$ において $\theta$ と $\cos\theta$ は $1$ 対 $1$ 対応するので、$\theta$ そのものの大小を考えづらい場合は、$\cos\theta$ についての大小を考えることが有効な場合が多いです。
まとめ
今回は、神戸大学理系数学(2019年 第2問)の解説をしました。
ほかの問題にもチャレンジしよう!
神戸大学 理系数学 2019年 第1問 解説
神戸大学 理系数学 2019年 第2問 解説
神戸大学 理系数学 2019年 第3問 解説
神戸大学 理系数学 2019年 第4問 解説
神戸大学 理系数学 2019年 第5問 解説













