神戸大学 理系数学 2020年[後期] 第2問 解説

今回は、神戸大学理系数学（2020年後期 第2問）の解説をしたいと思います。

問題

$a$ を $a\geqq 0$ をみたす実数とし，$xy$ 平面において不等式
$$0\leqq x\leqq e-1 \ \text{かつ} \ y\{y-\log(x+1)+a\}\leqq 0$$の表す部分の面積を $S(a)$ とする．以下の問に答えよ．

⑴　$S(a)$ を求めよ．

⑵　$S(a)$ の最小値を求めよ．

（神戸大学）

解答

⑴

$y\{y-\log(x+1)+a\}\leqq 0$ は「 $y\geqq 0$ かつ $y\leqq\log(x+1)-a$ 」または「 $y\leqq 0$ かつ $y\geqq\log(x+1)-a$ 」と同値である。

$$f(x)=\log(x+1)-a$$とおくと
$$f(x)=0 \ \Longleftrightarrow \ x=e^a-1$$であり
$$f(0)=-a\leqq 0,\quad f(e-1)=1-a$$となる。

(ⅰ)　$0\leqq a\lt 1$ のとき
$S(a)$ は下図の網掛け部分の面積である。

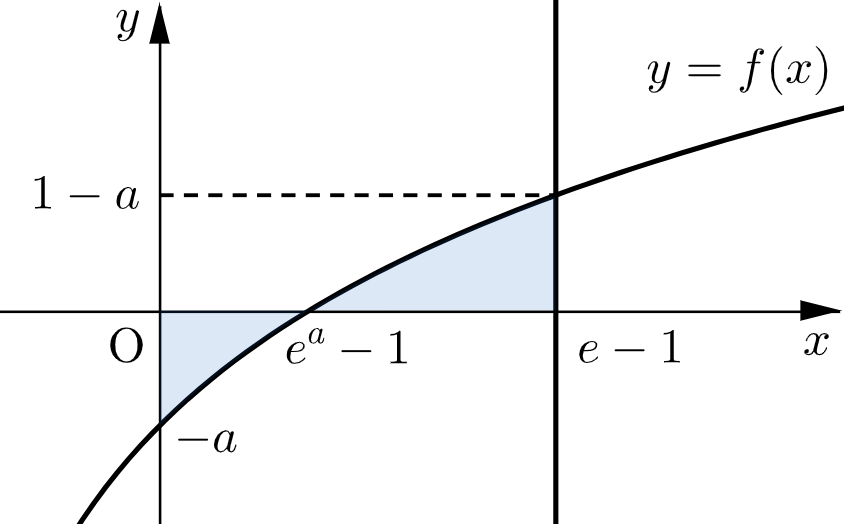
よって
$$\begin{align}
S(a) &= \displaystyle\int_{0}^{e^a-1}\{-\log(x+1)+a\}dx+\displaystyle\int_{e^a-1}^{e-1}\{\log(x+1)-a\}dx \\
&= \Big[-(x+1)\log(x+1)+(a+1)x\Big]_{0}^{e^a-1} \\
&\hphantom{=} \ \ +\Big[(x+1)\log(x+1)-(a+1)x\Big]_{e^a-1}^{e-1} \\
&= 2\{-ae^a+(a+1)(e^a-1)\}+e-(a+1)(e-1) \\[0.2em]
&= 2e^a-(e+1)a-1
\end{align}$$

(ⅱ)　$a\geqq 1$ のとき
$S(a)$ は下図の網掛け部分の面積である。

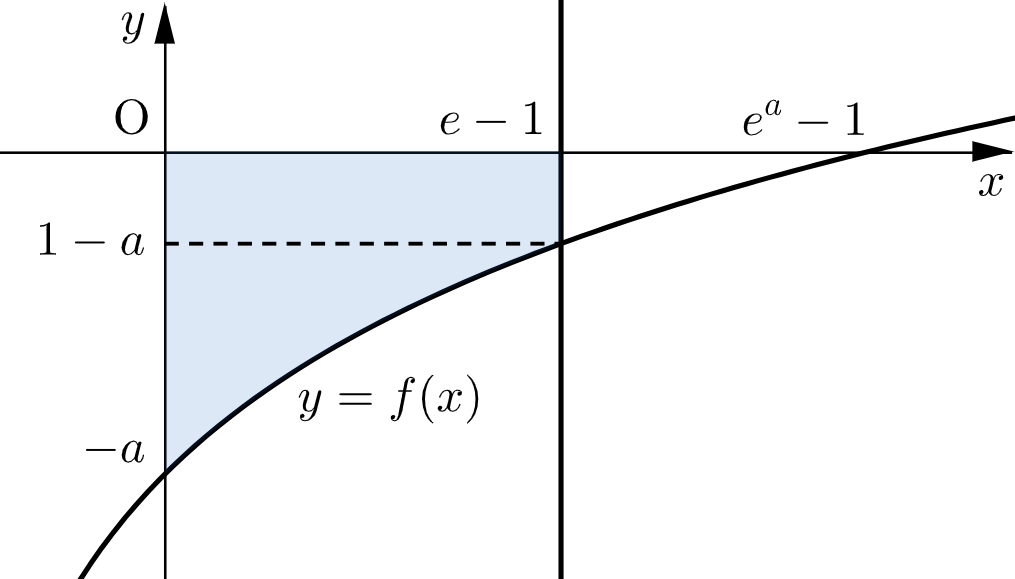
よって
$$\begin{align}
S(a) &= \displaystyle\int_{0}^{e-1}\{-\log(x+1)+a\}dx \\
&= \Big[-(x+1)\log(x+1)+(a+1)x\Big]_{0}^{e-1} \\
&= -e+(a+1)(e-1) \\[0.2em]
&= (e-1)a-1
\end{align}$$

(ⅰ),(ⅱ)より
$$S(a)=\left\{
\begin{array}{ll}
\boldsymbol{2e^a-(e+1)a-1} & \mathbf{\text{（}} \ \boldsymbol{0\leqq a\lt 1} \ \mathbf{\text{のとき）}} \\[0.3em]
\boldsymbol{(e-1)a-1} & \mathbf{\text{（}} \ \boldsymbol{a\geqq 1} \ \mathbf{\text{のとき）}}
\end{array}
\right.$$

⑵

(ⅰ)　$0\leqq a\lt 1$ のとき
$$S'(a)=2e^a-(e+1)$$となる。

$$S'(a)=0 \ \Longleftrightarrow \ a=\log\dfrac{e+1}{2}$$であり
$$\log\dfrac{1+1}{2}\lt\log\dfrac{e+1}{2}\lt\log\dfrac{e+e}{2}$$より
$$0\lt\log\dfrac{e+1}{2}\lt 1$$をみたす。

(ⅱ)　$a\geqq 1$ のとき
$$S'(a)=e-1\gt 0$$

(ⅰ),(ⅱ)より、$S(a)$ の増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c|c}\hline
a & 0 & \cdots & \log\dfrac{e+1}{2} & \cdots & 1 & \cdots \\ \hline
S'(a) & & – & 0 & + & & + \\ \hline
S(a) & & \searrow & \text{最小} & \nearrow & & \nearrow \\ \hline
\end{array}$$

したがって、$S(a)$ の最小値は
$$\begin{align}
S\left(\log\dfrac{e+1}{2}\right) &= 2\cdot\dfrac{e+1}{2}-(e+1)\log\dfrac{e+1}{2}-1 \\
&= \boldsymbol{e-(e+1)\log\dfrac{e+1}{2}}
\end{align}$$

解説

まず、問題文の不等式が $xy$ 平面上でどのような領域を表しているのか把握するのがポイントです。

⑴は、$a$ の範囲によって $S(a)$ の表し方を分けたら、あとは積分計算です。

$\displaystyle\int\log x=x\log x-x+C$ は必ず覚えておきたい事項です。

⑵は、⑴で分けた範囲ごとに微分して増減表を書けば大丈夫です。
解答のように、(ⅰ),(ⅱ)をまとめて書くと、見た目もスッキリしますし、$a=\log\dfrac{e+1}{2}$ で最小値をとることが一発で分かります。

まとめ

今回は、神戸大学理系数学（2020年後期 第2問）の解説をしました。