今回は、東京大学理系数学(2020年 第3問)の解説をしたいと思います。
問題
$-1\leqq t\leqq 1$ を満たす実数 $t$ に対して,
$$\begin{align}
x(t) &= (1+t)\sqrt{1+t} \\
y(t) &= 3(1+t)\sqrt{1-t}
\end{align}$$とする。座標平面上の点 $\mathrm{P}(x(t), \ y(t))$ を考える。⑴ $-1\lt t\leqq 1$ における $t$ の関数 $\dfrac{y(t)}{x(t)}$ は単調に減少することを示せ。
⑵ 原点と $\mathrm{P}$ の距離を $f(t)$ とする。$-1\leqq t\leqq 1$ における $t$ の関数 $f(t)$ の増減を調べ,最大値を求めよ。
⑶ $t$ が $-1\leqq t\leqq 1$ を動くときの $\mathrm{P}$ の軌跡を $C$ とし,$C$ と $x$ 軸で囲まれた領域を $D$ とする。原点を中心として $D$ を時計回りに $90^{\circ}$ 回転させるとき,$D$ が通過する領域の面積を求めよ。
(東京大学)
解答
⑴
$$\begin{align}
\dfrac{y(t)}{x(t)} &= \dfrac{3(1+t)\sqrt{1-t}}{(1+t)\sqrt{1+t}} \\
&= 3\sqrt{\dfrac{1-t}{1+t}} \\
&= 3\sqrt{\dfrac{2}{1+t}-1}
\end{align}$$より、$-1\lt t\leqq 1$ において $\dfrac{y(t)}{x(t)}$ は単調に減少する。$$\tag{証明終}$$
⑵
$$\begin{align}
f(t) &= \sqrt{\{x(t)\}^2+\{y(t)\}^2} \\
&= \sqrt{\{(1+t)\sqrt{1+t}\}^2+\{3(1+t)\sqrt{1-t}\}^2} \\
&= (1+t)\sqrt{10-8t}
\end{align}$$より
$$\begin{align}
f'(t) &= \sqrt{10-8t} + (1+t)\cdot\dfrac{-8}{2\sqrt{10-8t}} \\
&= \dfrac{6-12t}{\sqrt{10-8t}}
\end{align}$$であるから、$f(t)$ の増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c}\hline
t & -1 & \cdots & \dfrac{1}{2} & \cdots & 1 \\ \hline
f'(t) & & + & 0 & – & \\ \hline
f(t) & 0 & \nearrow & \dfrac{3\sqrt{6}}{2} & \searrow & 2\sqrt{2} \\ \hline
\end{array}$$
よって、$f(t)$ は $t=\dfrac{1}{2}$ で最大値 $\boldsymbol{\dfrac{3\sqrt{6}}{2}}$ をとる。
$$\boldsymbol{\dfrac{3\sqrt{6}}{2}}$$
⑶
$-1\leqq t \leqq 1$ において $x(t)=(1+t)^{\frac{3}{2}}$ は単調増加する。
また $-1\lt t \lt 1$ において
$$\begin{align}
\dfrac{dy}{dt} &= 3\sqrt{1-t}+3(1+t)\dfrac{-1}{2\sqrt{1-t}} \\
&= \dfrac{3(1-3t)}{2\sqrt{1-t}}
\end{align}$$より、$x(t), \ y(t)$ の増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c}\hline
t & -1 & \cdots & \dfrac{1}{3} & \cdots & 1 \\ \hline
\dfrac{dx}{dt} & & + & & + & \\ \hline
\dfrac{dy}{dt} & & + & 0 & – & \\ \hline
x(t) & 0 & \nearrow & \dfrac{8\sqrt{3}}{9} & \nearrow & 2\sqrt{2} \\ \hline
y(t) & 0 & \nearrow & \dfrac{4\sqrt{6}}{3} & \searrow & 0 \\ \hline
\end{array}$$
さらに⑴より、原点を $\mathrm{O}$ とすると、直線 $\mathrm{OP}$ の傾きは単調に減少するので、$C,D$ の概形は図のようになる。
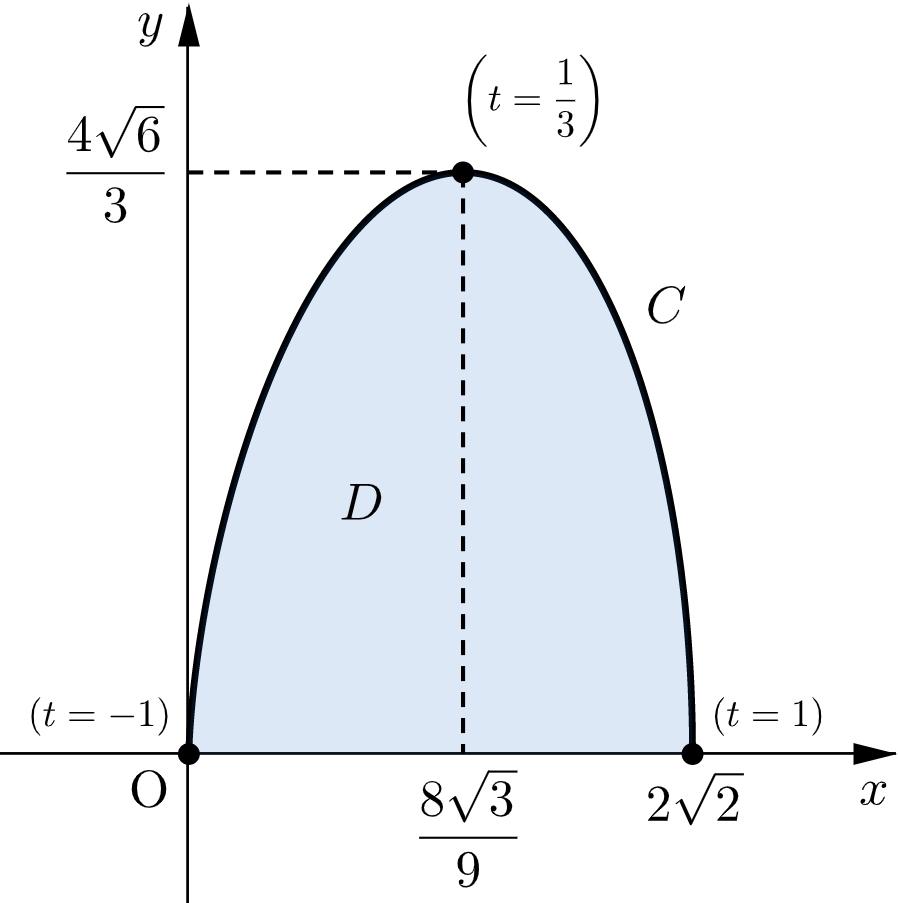
$D$ が通過する領域は図の網掛け部分(境界を含む)である。
ここで、$t=\dfrac{1}{2}$ における点 $\mathrm{P}$ の位置を $\mathrm{Q}$ とし、点 $\mathrm{Q}$ および曲線 $C$ を原点を中心として時計回りに $90^{\circ}$ 回転したものをそれぞれ $\mathrm{Q}’,C’$ とする。
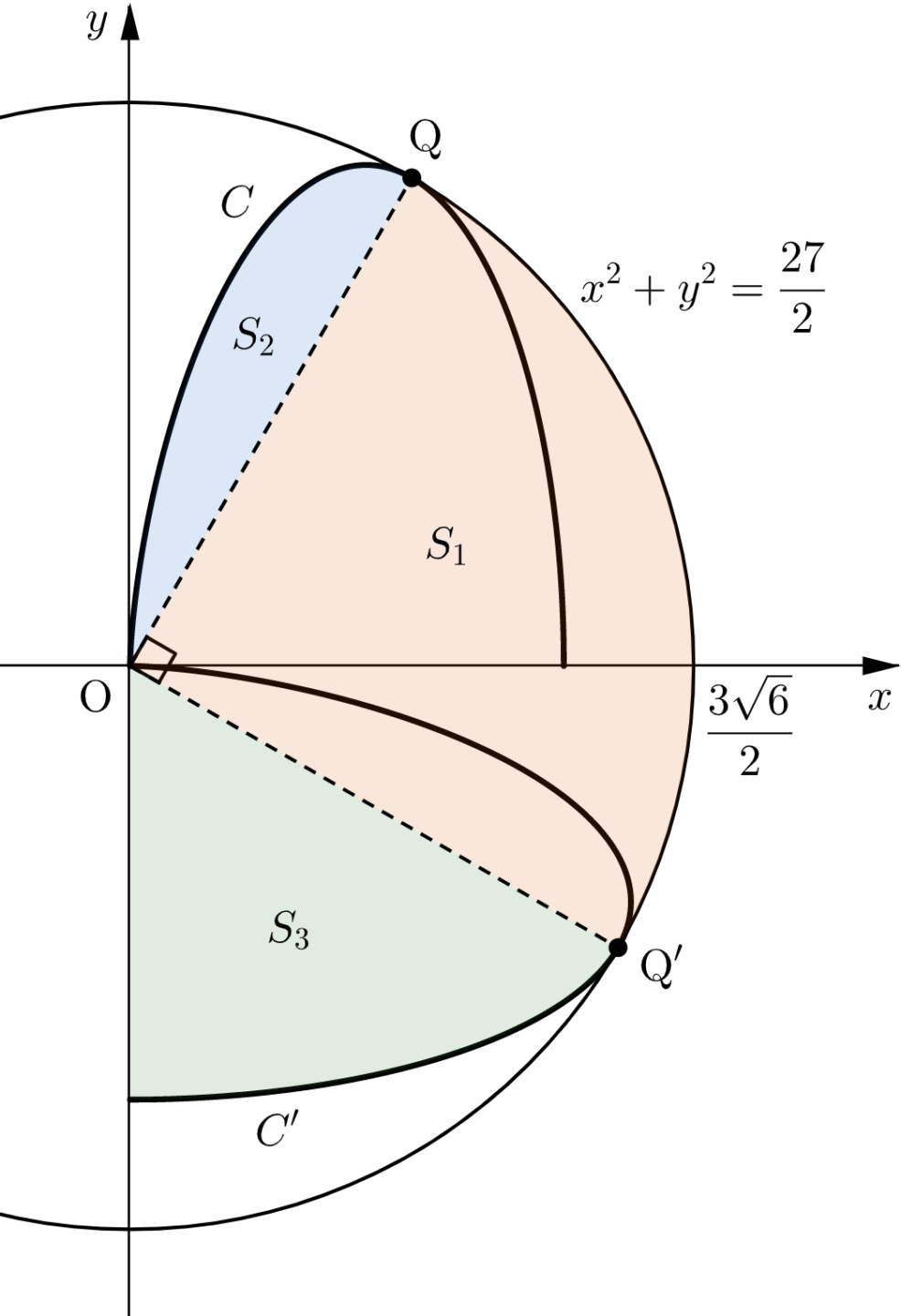
このとき、線分 $\mathrm{OQ}, \ \mathrm{OQ}’$ と円 $x^2+y^2=\dfrac{27}{2}$ で囲まれた領域の面積を $S_1$ とすると、$S_1$ は半径 $\dfrac{3\sqrt{6}}{2}$ の円の $\dfrac{1}{4}$ の面積に等しく
$$S_1 = \dfrac{1}{4}\cdot\pi\cdot \dfrac{27}{2} = \dfrac{27}{8}\pi$$
また、線分 $\mathrm{OQ}$ と曲線 $C$ で囲まれた領域の面積を $S_2$、線分 $\mathrm{OQ}’$ と曲線 $C’$ および $y$ 軸で囲まれた領域の面積を $S_3$ とすると、$S_2+S_3$ は領域 $D$ の面積に等しく
$$\begin{align}
S_2+S_3 &= \displaystyle\int_{0}^{2\sqrt{2}} y \ dx = \displaystyle\int_{-1}^{1} y(t)\dfrac{dx(t)}{dt}dt \\
&= \displaystyle\int_{-1}^{1} 3(1+t)\sqrt{1-t}\cdot\dfrac{3}{2}\sqrt{1+t}dt \\
&= \dfrac{9}{2}\displaystyle\int_{-1}^{1}\left\{ \sqrt{1-t^2}dt + t\sqrt{1-t^2} \right\}dt
\end{align}$$
ここで、$\displaystyle\int_{-1}^{1} \sqrt{1-t^2}dt$ は半径 $1$ の円の $\dfrac{1}{2}$ の面積に等しく
$$\displaystyle\int_{-1}^{1} \sqrt{1-t^2}dt = \dfrac{1}{2}\pi$$
また、$(-t)\sqrt{1-(-t)^2} = -t\sqrt{1-t^2}$ より、$t\sqrt{1-t^2}$ は奇関数なので
$$\displaystyle\int_{-1}^{1} t\sqrt{1-t^2}dt = 0$$
よって
$$S_2+S_3=\dfrac{9}{2}\cdot\left( \dfrac{1}{2}\pi+0 \right) = \dfrac{9}{4}\pi$$
したがって、$D$ が通過する領域の面積は
$$S_1+S_2+S_3 = \dfrac{27}{8}\pi + \dfrac{9}{4}\pi = \boldsymbol{\dfrac{45}{8}\pi}$$
$$\boldsymbol{\dfrac{45}{8}\pi}$$
解説
この問題は、$D$ が通過する領域の面積が $S_1,S_2,S_3$ の $3$ つに分けられることに気付けるかどうかがポイントでした。さらに $S_1$ が中心角 $90^\circ$ の扇形であり、$S_2+S_3$ が領域 $D$ そのものの面積に等しいことがイメージできれば、あとは計算だけです。
回転する領域の面積を求めるにあたって、中心からの距離の増減・最大値が必要なことは明らかなので⑵を使うことは分かりますが、⑴がどこに活かされているか分かりましたか?
実は、⑴の事実があることで、$C$ が「膨らんでいる」状態を表すことができます。$C$ が線分 $\mathrm{OQ}$ にめり込む(横切る)ような曲線だったとすると、$D$ の通過領域面積は $S_1+S_2+S_3$ と表せなくなってしまいます。
このことから⑴が必要だったのです。
また先ほど「あとは計算」と言いましたが、積分の計算で奇関数を見抜くなど、計算時間と計算ミスを減らせるポイントがあるので、ぜひ気付けるように注意しましょう。
まとめ
今回は、東京大学理系数学(2020年 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2020年 第1問 解説
東京大学 理系数学 2020年 第2問 解説
東京大学 理系数学 2020年 第3問 解説
東京大学 理系数学 2020年 第4問 解説
東京大学 理系数学 2020年 第5問 解説
東京大学 理系数学 2020年 第6問 解説













