神戸大学 理系数学 2022年[後期] 第4問 解説

今回は、神戸大学理系数学（2022年後期 第4問）の解説をしたいと思います。

問題

媒介変数表示 $x=\sin t, \ $$y=-\cos 2t-2\cos t-1$$\text{（} \ 0\leqq t\leqq\pi \ \text{）}$で表される曲線を $C$ とする．以下の問に答えよ．

⑴　$\dfrac{dx}{dt}=0$ または $\dfrac{dy}{dt}=0$ となる $t$ の値を求めよ．

⑵　$C$ の概形をかけ．

⑶　$C$ と $y$ 軸で囲まれた図形を $y$ 軸の周りに $1$ 回転してできる立体の体積を求めよ．

（神戸大学）

解答

⑴

$$\dfrac{dx}{dt}=\cos t$$より
$$\dfrac{dx}{dt}=0 \ \Longleftrightarrow \ t=\boldsymbol{\dfrac{\pi}{2}}$$

また
$$\begin{align}
\dfrac{dy}{dt} &= 2\sin 2t+2\sin t \\
&= 4\sin t\cos t+2\sin t \\[0.3em]
&= 2\sin t(2\cos t+1)
\end{align}$$より
$$\begin{align}
\dfrac{dy}{dt}=0 \ &\Longleftrightarrow \ \sin t=0, \ \cos t=-\dfrac{1}{2} \\
&\Longleftrightarrow \ t=\mathbf{0}, \ \boldsymbol{\dfrac{2}{3}\pi}, \ \boldsymbol{\pi}
\end{align}$$

⑵

$(x,y)$ の増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c|c|c}\hline
t & 0 & \cdots & \dfrac{\pi}{2} & \cdots & \dfrac{2}{3}\pi & \cdots & \pi \\ \hline
\dfrac{dx}{dt} & & + & 0 & – & – & – & \\ \hline
\dfrac{dy}{dt} & (0) & + & + & + & 0 & – & (0) \\ \hline
x & 0 & \nearrow & 1 & \searrow & \dfrac{\sqrt{3}}{2} & \searrow & 0 \\ \hline
y & -4 & \nearrow & 0 & \nearrow & \dfrac{1}{2} & \searrow & 0 \\ \hline
\end{array}$$

よって、$C$ の概形は下図のようになる。

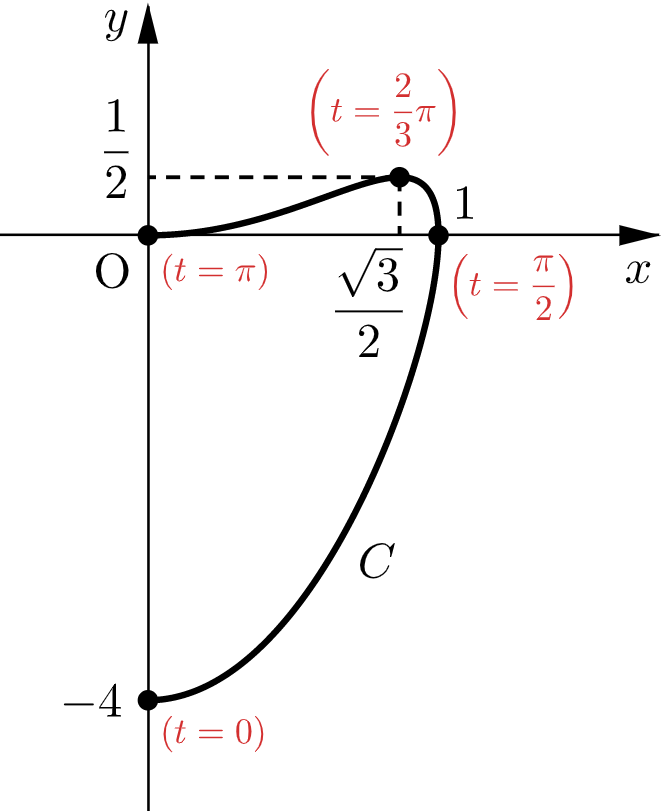
⑶

⑵より、求める体積 $V$ は
$$\begin{align}
V &= \displaystyle\int_{-4}^{\frac{1}{2}}\pi x^2dy-\displaystyle\int_{0}^{\frac{1}{2}}\pi x^2dy \\
&= \displaystyle\int_{0}^{\frac{2}{3}\pi}\pi x^2\dfrac{dy}{dt}dt-\displaystyle\int_{\pi}^{\frac{2}{3}\pi}\pi x^2\dfrac{dy}{dt}dt \\
&= \displaystyle\int_{0}^{\pi}\pi x^2\dfrac{dy}{dt}dt \\
&= \pi\displaystyle\int_{0}^{\pi}\sin^2t\cdot 2\sin t(2\cos t+1)dt \\
&= 2\pi\displaystyle\int_{0}^{\pi}(\cos^2t-1)(2\cos t+1)(-\sin t)dt \\
&= 2\pi\displaystyle\int_{0}^{\pi}(2\cos^3t+\cos^2t-2\cos t-1)(-\sin t)dt \\
&= 2\pi\left[\dfrac{1}{2}\cos^4t+\dfrac{1}{3}\cos^3t-\cos^2t-\cos t\right]_{0}^{\pi} \\
&= \boldsymbol{\dfrac{8}{3}\pi}
\end{align}$$

解説

いきなり⑶を聞かれたとしても、自分で⑴,⑵の行程を踏めるよう、媒介変数表示された曲線の面積や体積を求める問題に関しては手順を押さえておきましょう。

⑶で $V$ を求める際、いきなり $\displaystyle\int_{0}^{\pi}$ としてはいけません。計算の結果、媒介変数がつながったという過程を見せる必要があります。

また、三角関数の積分で大量の $\cos$ と $1$ つだけの $\sin$ がつくれるときは、合成関数の微分を利用するチャンスなので、見落とさず計算量を減らせるようにしましょう。

まとめ

今回は、神戸大学理系数学（2022年後期 第4問）の解説をしました。