今回は、神戸大学理系数学(2022年後期 第2問)の解説をしたいと思います。
問題
$z$ を実数でない複素数,$\mathrm{A}(z), \ $$\mathrm{B}(z^2), \ $$\mathrm{C}(z^3)$ を複素数平面上の $3$ 点とする.以下の問に答えよ.
⑴ $3$ 点 $\mathrm{A},\mathrm{B},\mathrm{C}$ は一直線上にないことを示せ.
⑵ $w$ を $w\ne 0,1$ である複素数,$\mathrm{O}(0), \ $$\mathrm{P}(1), \ $$\mathrm{Q}(w)$ を複素数平面上の $3$ 点とし,$\angle\mathrm{ABC}=\angle\mathrm{OPQ}, \ $$\angle\mathrm{BAC}=\angle\mathrm{POQ}$ とする.$w$ の値を $z$ を用いて表せ.ただし,角は向きを含めて考える.
⑶ $\triangle\mathrm{ABC}$ が直角二等辺三角形になるときの $z$ の値を求めよ.
(神戸大学)
解答
⑴
$$\begin{align}
\dfrac{z^3-z}{z^2-z} &= \dfrac{z(z+1)(z-1)}{z(z-1)} \\
&= z+1 \quad\cdots\text{①}
\end{align}$$
$z$ は実数でないので、①より $\dfrac{z^3-z}{z^2-z}$ も実数でない。
したがって、$\angle\mathrm{BAC}\ne 0^\circ,180^\circ$ より、$3$ 点 $\mathrm{A},\mathrm{B},\mathrm{C}$ は一直線上にない。$$\tag{証明終}$$
⑵
$\angle\mathrm{ABC}=\angle\mathrm{OPQ}, \ $$\angle\mathrm{BAC}=\angle\mathrm{POQ}$ より
$$\begin{align}
&\left\{
\begin{aligned}
\arg\dfrac{z^3-z^2}{z-z^2} &= \arg\dfrac{w-1}{0-1} \\
\arg\dfrac{z^3-z}{z^2-z} &= \arg\dfrac{w-0}{1-0}
\end{aligned}
\right. \\[0.3em]
\Longleftrightarrow \ &\left\{
\begin{alignedat}{2}
\arg(-z) &= \arg(1-w) & &\quad\cdots\text{②} \\
\arg(z+1) &= \arg w & &\quad\cdots\text{③}
\end{alignedat}
\right.
\end{align}$$
③より、実数 $k$ を用いて
$$w=k(z+1) \quad\cdots\text{④}$$と表せ、これを②に代入すると
$$\begin{align}
\arg(-z) &= \arg\{1-k(z+1)\} \\
&= \arg(-kz-k+1)
\end{align}$$となる。すなわち、同様に実数 $\ell$ を用いて
$$-kz-k+1=\ell(-z)$$と表せ、$z\ne 0$ より、$\dfrac{kz+k-1}{z}$ は実数となる。
よって
$$\begin{align}
\dfrac{kz+k-1}{z} &= \overline{\left(\dfrac{kz+k-1}{z}\right)} \\
\dfrac{kz+k-1}{z} &= \dfrac{k\overline{z}+k-1}{\overline{z}} \\
1+\dfrac{k-1}{z} &= 1+\dfrac{k-1}{\overline{z}} \\
\therefore \ (k-1)(z-\overline{z}) &= 0
\end{align}$$$z$ は実数でないので $z\ne\overline{z}$ であるから、$k=1$ となる。
したがって、④より
$$w=\boldsymbol{z+1}$$
$$\boldsymbol{z+1}$$
⑶
⑵の $3$ 点 $\mathrm{O},\mathrm{P},\mathrm{Q}$ を考えると、$\triangle\mathrm{ABC} \backsim \triangle\mathrm{OPQ}$ なので、$\triangle\mathrm{ABC}$ が直角二等辺三角形になることは $\triangle\mathrm{OPQ}$ が直角二等辺三角形になることと同値である。
$\triangle\mathrm{OPQ}$ が直角二等辺三角形になるとき、
$$\{|\angle\mathrm{OPQ}|,|\angle\mathrm{POQ}|,|\angle\mathrm{OQP}|\}=\{90^\circ,45^\circ,45^\circ\}$$のすべての組み合わせを考えると、下図より
$$w=\pm i, \ \dfrac{1}{2}\pm\dfrac{1}{2}i, \ 1\pm i$$となる。
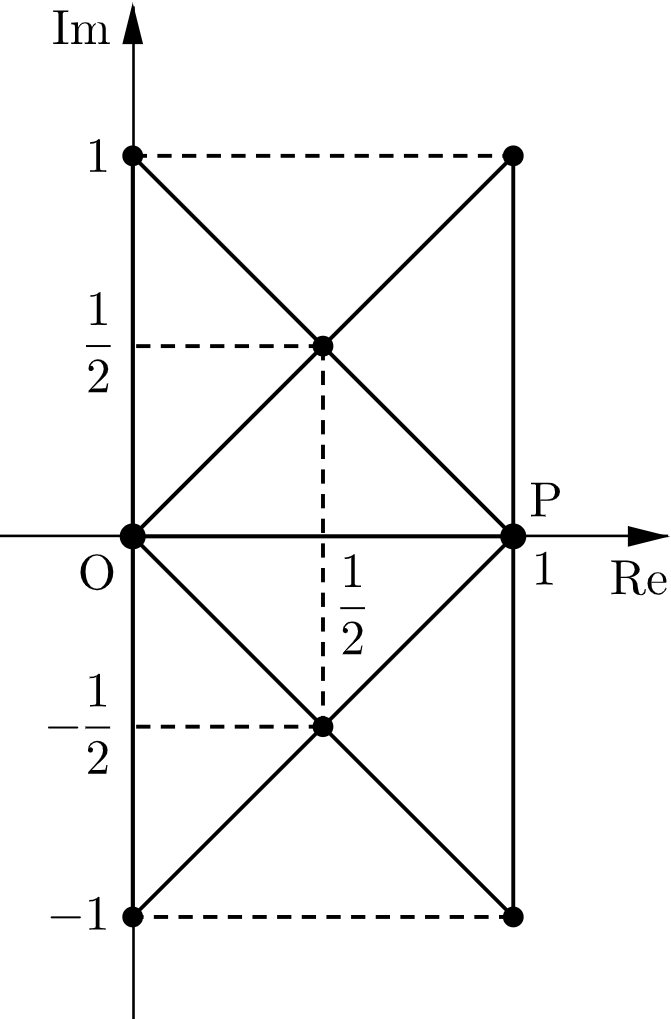
⑵より $z=w-1$ であるから
$$z=\boldsymbol{-1\pm i}, \ \boldsymbol{-\dfrac{1}{2}\pm\dfrac{1}{2}i}, \ \boldsymbol{\pm i}$$
$$\boldsymbol{-1\pm i}, \ \boldsymbol{-\dfrac{1}{2}\pm\dfrac{1}{2}i}, \ \boldsymbol{\pm i}$$
解説
この問題は、いきなり⑶だけを聞かれるとキツいですが、⑴,⑵でうまく誘導がされているので、それに乗っかれば自然と答えにたどり着けるようになっています。
⑴は、ベクトルと同様に考えましょう。基本的な問題です。
⑵は、偏角どうしが等しいことをどう処理するかがポイントです。
⑶は、⑵で等しい角度に関する処理を終えているので、考えやすい $\triangle\mathrm{OPQ}$ を使って解き進めましょう。
点 $\mathrm{Q}$ の位置は、解答のように最低限の記述と図があれば十分だと思います。
まとめ
今回は、神戸大学理系数学(2022年後期 第2問)の解説をしました。
ほかの問題にもチャレンジしよう!
神戸大学 理系数学 2022年[後期] 第1問 解説
神戸大学 理系数学 2022年[後期] 第2問 解説
神戸大学 理系数学 2022年[後期] 第3問 解説
神戸大学 理系数学 2022年[後期] 第4問 解説
神戸大学 理系数学 2022年[後期] 第5問 解説













