今回は、一橋大学数学(2021年後期 第5問)の解説をしたいと思います。
問題
次の [Ⅰ],[Ⅱ] のいずれか一方を選択して解答せよ。
[Ⅰ] $x,\,y$ は実数とする。$y\gt x^n$ を満たす正の整数 $n$ が存在する点 $(x,\,y)$ 全体の集合を,$xy$ 平面上に図示せよ。
[Ⅱ] $f(x)$ は微分可能かつ導関数が連続な関数とする。$f(0)=0$ であるとき
(一橋大学)
$$\dfrac{d}{dx}\left(\displaystyle\int_{0}^{x}e^{-t}f(x-t)dt\right)=\displaystyle\int_{0}^{x}e^{-t}f'(x-t)dt$$を示せ。
解答
[Ⅰ]
(ⅰ) $x\lt-1$ のとき
・$y\geqq-1$ のとき、$n=1$ とすれば成り立つ。
・$y\lt-1$ のとき、$x’=-x$,$y’=-y$ とすると $x’\gt1$,$y’\gt1$ であり、$n$ を奇数とすると
$$\begin{alignat}{2}
&& y &\gt x^n \\
\Longleftrightarrow \ && -y’ &\gt (-x’)^n=-{x’}^n \\
\Longleftrightarrow \ && y’ &\lt {x’}^n \\
\Longleftrightarrow \ && \log_{x’}y’ &\lt n \quad\cdots\text{①}
\end{alignat}$$となり、$n$ を十分大きくすれば①が成り立つ。
よって、任意の $y$ に対して与式を満たす $n$ が存在する。
(ⅱ) $-1\leqq x\leqq0$ のとき
$x^n\geqq x$ より、$y\leqq x$ のときは与式を満たす $n$ は存在せず、$y\gt x$ のときは $n=1$ とすれば与式が成り立つ。
(ⅲ) $0\lt x\lt1$ のとき
$$y\gt x^n \ \Longleftrightarrow \ \log_{x}y \lt n \quad\cdots\text{②}$$となり、$n$ を十分大きくすれば②が成り立つ。
よって、任意の $y$ に対して与式を満たす $n$ が存在する。
(ⅳ) $1\lt x$ のとき
$x^n\geqq x$ より、$y\leqq x$ のときは与式を満たす $n$ は存在せず、$y\gt x$ のときは $n=1$ とすれば与式が成り立つ。
(ⅰ)~(ⅳ)より、求める集合を図示すると、下図の網掛け部分のようになる。ただし、境界は含まない。
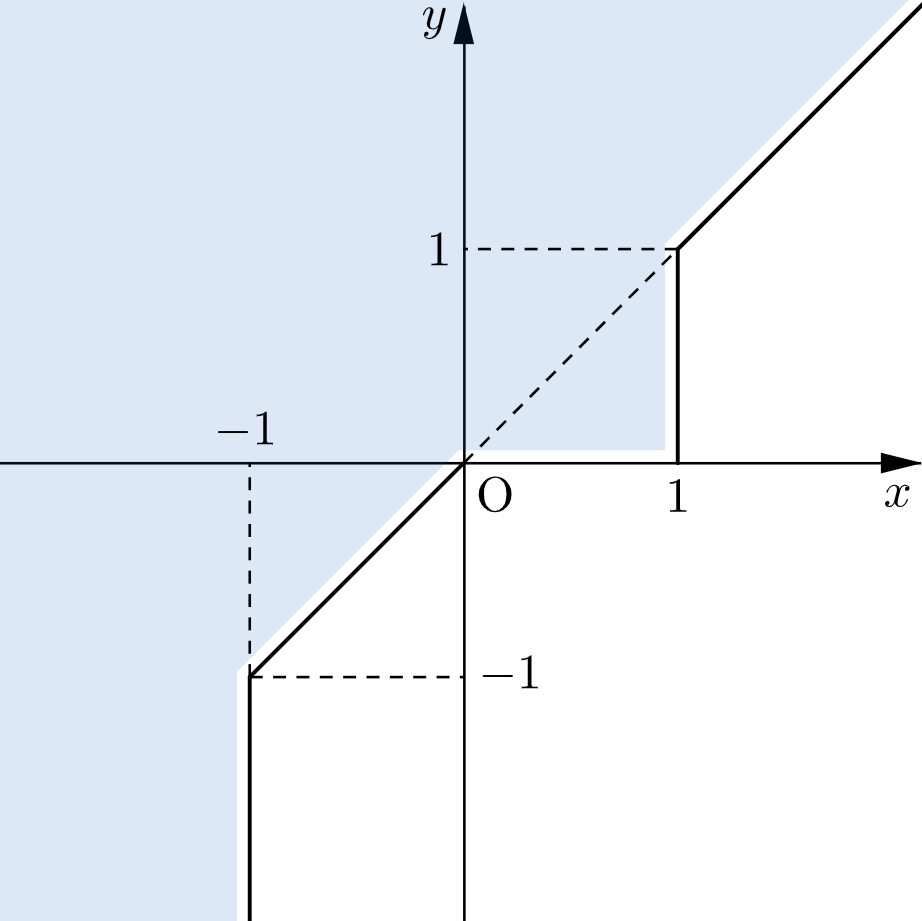
下図の網掛け部分(境界は含まない)

[Ⅱ]
部分積分により
$$\begin{align}
&\hphantom{=} \ \ \displaystyle\int_{0}^{x}e^{-t}f(x-t)dt \\
&= \Big[-e^{-t}f(x-t)\Big]_{0}^{x}-\displaystyle\int_{0}^{x}\{-e^{-t}f'(x-t)\cdot(x-t)’\}dt \\
&= f(x)-\displaystyle\int_{0}^{x}e^{-t}f'(x-t)dt \quad\cdots\text{①} \\[0.2em]
&\hphantom{=} \text{(}\because f(0)=0\,\text{)}
\end{align}$$
ここで、$\displaystyle\int_{0}^{x}e^{-t}f'(x-t)dt$ について
$$x-t=u$$とおくと
$$dt=-du \qquad
\begin{array}{c|c} \hline
t & 0 \to x \\ \hline
u & x \to 0 \\ \hline
\end{array}$$より
$$\begin{align}
\displaystyle\int_{0}^{x}e^{-t}f'(x-t)dt &= \displaystyle\int_{x}^{0}e^{u-x}f'(u)(-du) \\
&= \displaystyle\int_{0}^{x}e^{u-x}f'(u)du \\
&= \displaystyle\int_{0}^{x}e^{t-x}f'(t)dt \\
&= e^{-x}\displaystyle\int_{0}^{x}e^{t}f'(t)dt \quad\cdots\text{②}
\end{align}$$となるので、①より
$$\begin{align}
\displaystyle\int_{0}^{x}e^{-t}f(x-t)dt &= f(x)-e^{-x}\displaystyle\int_{0}^{x}e^{t}f'(t)dt
\end{align}$$となる。
両辺を $x$ について微分すると
$$\begin{align}
&\hphantom{=} \ \ \dfrac{d}{dx}\left(\displaystyle\int_{0}^{x}e^{-t}f(x-t)dt\right) \\
&= f'(x)+e^{-x}\displaystyle\int_{0}^{x}e^{t}f'(t)dt-e^{-x}\cdot e^{x}f'(x) \\
&= e^{-x}\displaystyle\int_{0}^{x}e^{t}f'(t)dt \\
&= \displaystyle\int_{0}^{x}e^{-t}f'(x-t)dt \ \text{(}\because\text{②)}
\end{align}$$となるので、題意は示された。$$\tag{証明終}$$
解説
[Ⅰ]
題意を正確に理解するところが最大のポイントです。
つまり、ある点 $(x_1,\,y_1)$ について、$y_1\gt{x_1}^n$ を満たす正の整数 $n$ が $1$ つでもあれば、点 $(x_1,\,y_1)$ は求める集合に含まれる、ということです。
平面を象限ごとに区切って場合分けする方法もありますが、与式の形から $x$ の値で場合分けした方がシンプルだと判断したため、本解答ではそのように場合分けしてあります。
特に $x$ や $y$ の符号が負になると混乱しやすいので、落ち着いて解きましょう。
もし文字式で判断できなければ、$-\dfrac{1}{2}$ など具体的な値を代入して判断しましょう。
[Ⅱ]
与式左辺の被微分関数をいきなり置換積分しようとすると、$f(0)=0$ の使いどころがなく、与式右辺に出てくる $f'(x-t)$ も現れません。
そこで、置換積分ではなく部分積分をしてみると、$f(x-t)$ に $t=x$ を代入する際に $f(0)=0$ が使えますし、$f'(x-t)$ も現れるようになります。
また、定積分の微分に関する公式
$$\dfrac{d}{dx}\left(\displaystyle\int_{0}^{x}f(t)dt\right)=f(x)$$を使う際には、$f(t)$ の式の中に $x$ が入っていてはいけません。
そのため、置換積分をして被積分関数を $t$ だけの式にする必要があります。
置換積分や部分積分など、微分・積分に関する計算手法をマスターしていなければ解けない問題です。
まとめ
今回は、一橋大学数学(2021年後期 第5問)の解説をしました。
ほかの問題にもチャレンジしよう!
一橋大学 数学 2021年[後期] 第1問 解説
一橋大学 数学 2021年[後期] 第2問 解説
一橋大学 数学 2021年[後期] 第3問 解説
一橋大学 数学 2021年[後期] 第4問 解説
一橋大学 数学 2021年[後期] 第5問 解説













