一橋大学 数学 2021年[後期] 第4問 解説

今回は、一橋大学数学（2021年後期 第4問）の解説をしたいと思います。

問題

　箱の中に $1$ から $10$ までの番号が書かれた $10$ 枚のカードが入っている。箱から $1$ 枚のカードを取り出し，書かれた数の約数の個数を記録する。取り出したカードは箱に戻す。以上の操作をくり返し，記録された数の和が $3$ の倍数になったら終了する。$n$ 回目で終了する確率 $p_n$ を求めよ。

（一橋大学）

解答

カードの番号とその約数の個数、およびそれを $3$ で割った余りについてまとめると、下表のようになる。
$$\begin{array}{c|c|c|c|c|c|c|c|c|c|c} \hline
\text{番号} &1&2&3&4&5&6&7&8&9&10 \\ \hline
\text{約数の個数} &2&4&4&6&4&8&4&8&6&8 \\ \hline
3 \ \text{で割った余り} &2&1&1&0&1&2&1&2&0&2 \\ \hline
\end{array}$$

したがって、記録された数の和を $3$ で割った余りについては
・確率 $\dfrac{1}{5}$ で変化しない
・確率 $\dfrac{2}{5}$ で $1$ 足される（$\,2$ 引かれる）
・確率 $\dfrac{2}{5}$ で $2$ 足される（$\,1$ 引かれる）

ここで、$n$ 回目の試行後、記録された数の和を $3$ で割った余りが $1$ となる確率を $q_n$，余りが $2$ となる確率を $r_n$ とおく。

$q_r$，$r_n$ の $n$ 回目から $(n+1)$ 回目への推移は下図のようになる。

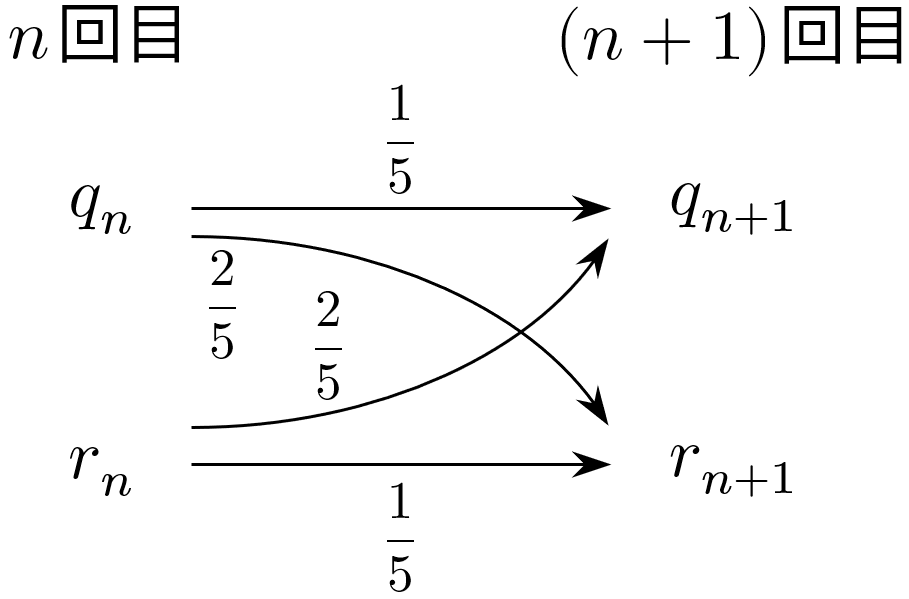
よって
$$\left\{\begin{align}
q_{n+1} &= \dfrac{1}{5}q_n+\dfrac{2}{5}r_n \\
r_{n+1} &= \dfrac{2}{5}q_n+\dfrac{1}{5}r_n
\end{align}\right.$$が成り立つ。

$2$ 式を足すと
$$\begin{align}
q_{n+1}+r_{n+1} &= \dfrac{3}{5}(q_n+r_n) \\
q_n+r_n &= (q_1+r_1)\left(\dfrac{3}{5}\right)^{n-1}
\end{align}$$ここで、$q_1=r_1=\dfrac{2}{5}$ であるから
$$q_n+r_n=\dfrac{4}{5}\left(\dfrac{3}{5}\right)^{n-1}$$となる。

したがって、$\boldsymbol{n\geqq2}$ のとき
$$\begin{align}
p_n &= \dfrac{2}{5}q_{n-1}+\dfrac{2}{5}r_{n-1} \\
&= \dfrac{2}{5}(q_{n-1}+r_{n-1}) \\
&= \dfrac{2}{5}\cdot\dfrac{4}{5}\left(\dfrac{3}{5}\right)^{n-2} \\[0.3em]
\therefore \ p_n &= \boldsymbol{\dfrac{8}{9}\left(\dfrac{3}{5}\right)^n}
\end{align}$$

また、$\boldsymbol{n=1}$ のとき
$$p_1=\boldsymbol{\dfrac{1}{5}}$$

別解

$\boldsymbol{n=1}$ のとき、$p_1=\boldsymbol{\dfrac{1}{5}}$ である。

以下、$n\geqq2$ とする。

ここで、記録された数の和を $3$ で割った余りが $0$ となる事象を $\mathrm{A}$，余りが $1$ または $2$ となる事象を $\mathrm{B}$ とすると、求める確率 $p_n$ は、$1\,$～$\,(n-1)$ 回目に事象 $\mathrm{B}$，$n$ 回目に事象 $\mathrm{A}$ が起きる確率である。

ここで、$1$ 回目に事象 $\mathrm{A}$ が起きる確率は $1-p_1=\dfrac{4}{5}$ である。

また、$k$ を $1\leqq k\leqq k-2$ を満たす整数とすると、$k$ 回目に事象 $\mathrm{B}$ が起きたとき、$(k+1)$ 回目に事象 $\mathrm{B}$ が起きる確率は $\dfrac{1}{5}+\dfrac{2}{5}=\dfrac{3}{5}$ である。

さらに、$(n-1)$ 回目に事象 $\mathrm{B}$ が起きたとき、$(k+1)$ 回目に事象 $\mathrm{A}$ が起きる確率は $\dfrac{2}{5}$ である。

以上より
$$\begin{align}
p_n &= \dfrac{4}{5}\cdot\left(\dfrac{3}{5}\right)^{n-2}\cdot\dfrac{2}{5} \\[0.3em]
\therefore \ p_n &= \boldsymbol{\dfrac{8}{9}\left(\dfrac{3}{5}\right)^n}\quad\boldsymbol{(n\geqq2)}
\end{align}$$

解説

確率漸化式に関する問題です。

記録された数の和が $3$ の倍数となると試行が終了してしまうので、$1\,$～$\,(n-1)$ 回目では和が $3$ の倍数とならないように注意しなければなりません。

今回の問題では、記録された数の和を $3$ で割った余りが「$\,1$ 足される確率」と「$\,2$ 足される確率」が等しいので、考えやすくなっています。

それを活かすと、別解のように確率漸化式を使わずとも、直接 $p_n$ を求めることができます。

まとめ

今回は、一橋大学数学（2021年後期 第4問）の解説をしました。