東京大学 理系数学 2019年 第5問 解説

今回は、東京大学理系数学（2019年 第5問）の解説をしたいと思います。

問題

　以下の問いに答えよ。

⑴　$n$ を $1$ 以上の整数とする。$x$ についての方程式
$$x^{2n-1}=\cos x$$は，ただ一つの実数解 $a_n$ をもつことを示せ。

⑵　⑴で定まる $a_n$ に対し，$\cos a_n\gt\cos1$ を示せ。

⑶　⑴で定まる数列 $a_1,a_2,a_3,\cdots\cdots,a_n,\cdots\cdots$ に対し，
$$\begin{align}
a &= \displaystyle\lim_{n\to\infty}a_n, \\[0.2em]
b &= \displaystyle\lim_{n\to\infty}a_n^n, \\[0.2em]
c &= \displaystyle\lim_{n\to\infty}\dfrac{a_n^n-b}{a_n-a}
\end{align}$$を求めよ。

（東京大学）

解答

⑴

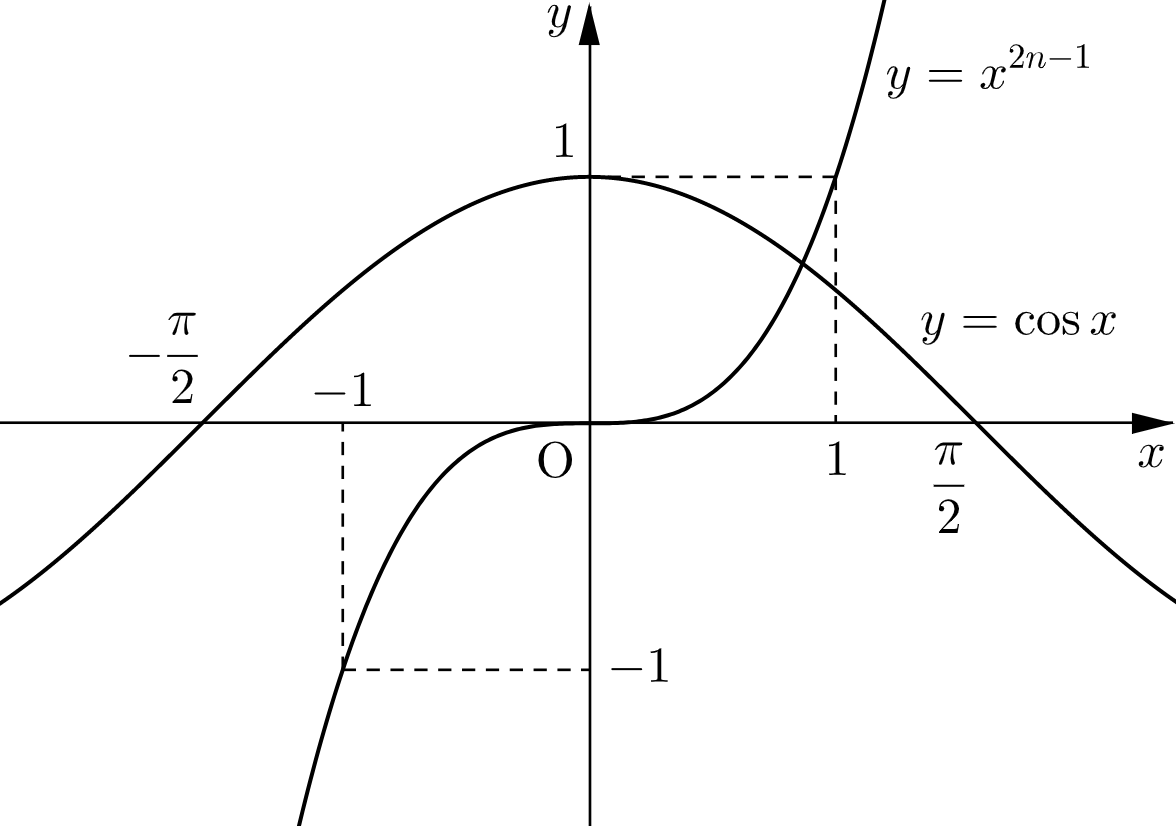
(ⅰ)　$|\,x\,|\gt1$ のとき

$|\,x\,|^{2n-1}\gt1$ より $|\,x^{2n-1}\,|\gt1$ であり、$|\,\cos x\,|\leqq1$ であるから、この区間において $x^{2n-1}\ne\cos x.$

(ⅱ)　$-1\leqq x\leqq0$ のとき

$2n-1$ は奇数なので $x^{2n-1}\leqq0$ であり、$\cos x\gt0$ であるから、この区間において $x^{2n-1}\ne\cos x.$

(ⅲ)　$0\lt x\leqq1$ のとき

$f(x)=x^{2n-1}-\cos x$ とおくと
$$\begin{align}
f'(x) &= (2n-1)x^{2n-2}+\sin x \\[0.2em]
&= (2n-1)(x^{n-1})^{2}+\sin x \gt0
\end{align}$$より、$f(x)$ は単調増加であり
$$f(0)=-1\lt0,\quad f(1)=1-\cos1\gt0$$となるので、この区間において $f(x)=0$ はただ $1$ つの実数解をもつ。

(ⅰ)～(ⅲ)より、題意は示された。$$\tag{証明終}$$

⑵

⑴より
$$0\lt a_n\lt1 \quad\cdots\text{①}$$であるから
$$\cos a_n\gt\cos1.$$$$\tag{証明終}$$

⑶

⑵の結果と①より
$$\begin{align}
a_n^{\,2n-1} &= \cos a_n \\
&\gt \cos1 \\
\therefore \ 1\gt a_n &\gt (\cos1)^{\frac{1}{2n-1}}.
\end{align}$$$$\displaystyle\lim_{n\to\infty}(\cos1)^{\frac{1}{2n-1}}=(\cos1)^0=1$$なので、はさみうちの原理により
$$a=\displaystyle\lim_{n\to\infty}a_n=\mathbf{1}.$$

また、$a_n^{\,2n-1}=\cos a_n$ より
$$a_n^{\,2n}=a_n\cos a_n$$であり、①の範囲において $a_n^{\,n}\gt0$ なので
$$a_n^{\,n}=\sqrt{a_n\cos a_n\vphantom{\cos^21}}$$よって
$$b=\displaystyle\lim_{n\to\infty}a_n^{\,n}=\boldsymbol{\sqrt{\cos1}}.$$

さらに
$$\begin{align}
c &= \displaystyle\lim_{n\to\infty}\dfrac{a_n^{\,n}-b}{a_n-a} \\
&= \displaystyle\lim_{n\to\infty}\dfrac{\sqrt{a_n\cos a_n\mathstrut}-\sqrt{\cos1\mathstrut}}{a_n-1}.
\end{align}$$

ここで、$\displaystyle\lim_{n\to\infty}a_n=1$ なので
$$c=\displaystyle\lim_{x\to1}\dfrac{\sqrt{x\cos x\mathstrut}-\sqrt{\cos1\mathstrut}}{x-1}$$と表せて、$g(x)=\sqrt{x\cos x\mathstrut}$ とおくと、微分係数の定義から
$$c=\displaystyle\lim_{x\to1}\dfrac{g(x)-g(1)}{x-1}=g'(1).$$

$g'(x)=\dfrac{\cos x-\sin x}{2\sqrt{x\cos x\mathstrut}}$ より
$$c=\boldsymbol{\dfrac{\cos1-\sin1}{2\sqrt{\cos1\mathstrut}}}.$$

解説

⑴は、$x=0,\,\pm\dfrac{\pi}{2}$ を境目として考えても示せますが、$x=0,\,\pm1$ を境目としておけば、⑵を少ない説明で証明することができます。

⑶は、極限計算にどれだけ慣れているかがカギで、さまざまなアプローチが考えられる中で適切なものを選ぶ力が試されています。

$c$ のように $\dfrac{\text{差}}{\text{差}}$ の極限は、微分係数の定義式を使って求めるものが時々あります。元の関数を定義式に合うように設定しましょう。

まとめ

今回は、東京大学理系数学（2019年 第5問）の解説をしました。