大阪大学 理系数学 2021年 第2問 解説

今回は、大阪大学理系数学（2021年 第2問）の解説をしたいと思います。

問題

　空間内に，同一平面上にない $4$ 点 $\mathrm{O},\mathrm{A},\mathrm{B},\mathrm{C}$ がある．$s,t$ を $0\lt s\lt 1, \ $$0\lt t\lt 1$ をみたす実数とする．線分 $\mathrm{OA}$ を $1:1$ に内分する点を $\mathrm{A}_0$，線分 $\mathrm{OB}$ を $1:2$ に内分する点を $\mathrm{B}_0$，線分 $\mathrm{AC}$ を $s:(1-s)$ に内分する点を $\mathrm{P}$，線分 $\mathrm{BC}$ を $t:(1-t)$ に内分する点を $\mathrm{Q}$ とする．さらに $4$ 点 $\mathrm{A}_0,\mathrm{B}_0,\mathrm{P},\mathrm{Q}$ が同一平面上にあるとする．

⑴　$t$ を $s$ を用いて表せ．

⑵　$|\overrightarrow{\mathrm{OA}}|=1, \ $$|\overrightarrow{\mathrm{OB}}|=|\overrightarrow{\mathrm{OC}}|=2, \ $$\angle\mathrm{AOB}=120^\circ, \ $$\angle\mathrm{BOC}=90^\circ, \ $$\angle\mathrm{COA}=60^\circ, \ $$\angle\mathrm{POQ}=90^\circ$ であるとき，$s$ の値を求めよ．

（大阪大学）

解答

⑴

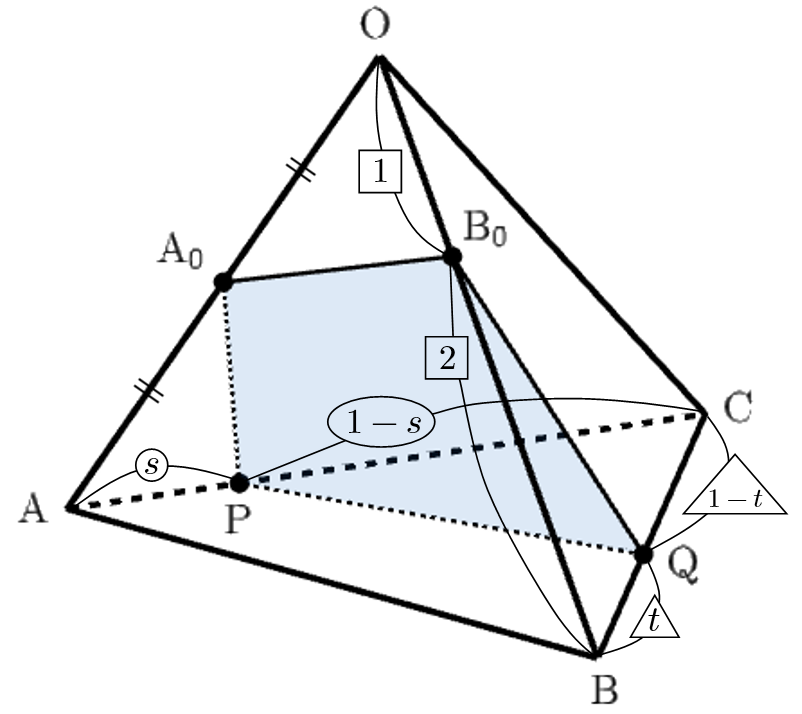
条件より
$$\begin{array}{l}
\overrightarrow{\mathrm{OA}_0} = \dfrac{1}{2}\overrightarrow{\mathrm{OA}},\quad \overrightarrow{\mathrm{OB}_0}=\dfrac{1}{3}\overrightarrow{\mathrm{OB}}, \\
\overrightarrow{\mathrm{OP}} = (1-s)\overrightarrow{\mathrm{OA}}+s\overrightarrow{\mathrm{OC}}, \\
\overrightarrow{\mathrm{OQ}} = (1-t)\overrightarrow{\mathrm{OB}}+t\overrightarrow{\mathrm{OC}} \quad\cdots\text{①}
\end{array}$$

また、点 $\mathrm{Q}$ は $3$ 点 $\mathrm{A}_0,\mathrm{B}_0,\mathrm{P}$ と同一平面上にあるので、実数 $k,\ell$ を用いて
$$\begin{eqnarray}
\overrightarrow{\mathrm{OQ}} &=& k\overrightarrow{\mathrm{OP}}+\ell\overrightarrow{\mathrm{OA}_0}+(1-k-\ell)\overrightarrow{\mathrm{OB}_0} \\
&=& k\{(1-s)\overrightarrow{\mathrm{OA}}+s\overrightarrow{\mathrm{OC}}\}+\ell\cdot\dfrac{1}{2}\overrightarrow{\mathrm{OA}}+(1-k-\ell) \cdot \dfrac{1}{3}\overrightarrow{\mathrm{OB}} \\
&=& \left\{ k(1-s)+\dfrac{1}{2}\ell \right\}\overrightarrow{\mathrm{OA}} + \dfrac{1}{3}(1-k-\ell)\overrightarrow{\mathrm{OB}} + ks\overrightarrow{\mathrm{OC}} \quad\cdots\text{②}
\end{eqnarray}$$と表せる。

$4$ 点 $\mathrm{O},\mathrm{A},\mathrm{B},\mathrm{C}$ は同一平面上にないので、$\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}},\overrightarrow{\mathrm{OC}}$ は一次独立である。したがって、①,②より
$$\left\{
\begin{eqnarray}
k(1-s)+\dfrac{1}{2}\ell &=& 0 \quad\cdots\text{③} \\
\dfrac{1}{3}(1-k-\ell) &=& 1-t \quad\cdots\text{④} \\
ks &=& t \quad\cdots\text{⑤} \\
\end{eqnarray}
\right.$$

③より $\ell = 2k(s-1)$ を④に代入すると
$$\begin{eqnarray}
\dfrac{1}{3}\{1-k-2k(s-1)\} &=& 1-t \\
1-k-2t+2k &=& 3(1-t) \ \text{（}\because\text{⑤）} \\
k &=& 2-t
\end{eqnarray}$$これを⑤に代入すると
$$\begin{eqnarray}
2s-st &=& t \\
(s+1)t &=& 2s \\
t &=& \boldsymbol{\dfrac{2s}{s+1}} \ \text{（}\because s+1\ne 0 \ \text{）}
\end{eqnarray}$$

⑵

$\angle\mathrm{POQ}=90^\circ$ より $\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}=0$ なので、⑴の結果を用いると
$$\begin{eqnarray}
\{(1-s)\overrightarrow{\mathrm{OA}}+s\overrightarrow{\mathrm{OC}}\} \cdot \left\{ \left(1-\dfrac{2s}{s+1}\right)\overrightarrow{\mathrm{OB}} + \dfrac{2s}{s+1}\overrightarrow{\mathrm{OC}} \right\} &=& 0 \\
\{(1-s)\overrightarrow{\mathrm{OA}}+s\overrightarrow{\mathrm{OC}}\} \cdot \{(1-s)\overrightarrow{\mathrm{OB}}+2s\overrightarrow{\mathrm{OC}}\} &=& 0
\end{eqnarray}$$$$(1-s)^2\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} +2s(1-s)\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} +s(1-s)\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}} +2s^2|\overrightarrow{\mathrm{OC}}|^2 = 0 \quad\cdots\text{⑥}$$

ここで
$$\begin{eqnarray}
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} &=& |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\angle\mathrm{AOB} \\
&=& 1 \cdot 2 \cdot \cos 120^\circ = -1 \\[0.5em]
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} &=& |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OC}}|\cos\angle\mathrm{COA} \\
&=& 1 \cdot 2 \cdot \cos 60^\circ = 1 \\[0.5em]
\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}} &=& |\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OC}}|\cos\angle\mathrm{BOC} \\
&=& 2 \cdot 2 \cdot \cos 90^\circ = 0
\end{eqnarray}$$であるから、⑥より
$$(1-s)^2\cdot(-1)+2s(1-s)\cdot 1 +s(1-s)\cdot 0 +2s^2\cdot 2^2 = 0$$$$\begin{eqnarray}
-1+2s-s^2+2s-2s^2+8s^2 &=& 0 \\
5s^2+4s-1 &=& 0 \\
(5s-1)(s+1) &=& 0 \\
s &=& \dfrac{1}{5},-1
\end{eqnarray}$$$0\lt s\lt 1$ より、$s=\boldsymbol{\dfrac{1}{5}}$ である。

解説

⑴は、$4$ 点 $\mathrm{A}_0,\mathrm{B}_0,\mathrm{P},\mathrm{Q}$ が同一平面上にあることから、実数 $k,\ell$ を用いて
$$\overrightarrow{\mathrm{OQ}} = k\overrightarrow{\mathrm{OP}}+\ell\overrightarrow{\mathrm{OA}_0}+(1-k-\ell)\overrightarrow{\mathrm{OB}_0}$$と表せることがポイントでした。
また連立方程式も文字が多くて厄介ですが、「 $t$ を $s$ を用いて表す」というゴールを見据えていれば消去すべき文字・残すべき文字が見えてくるのではないでしょうか。

⑵は、具体的な $s$ の値を求めなければならないので、点 $\mathrm{P},\mathrm{Q}$ に関する条件から攻めるのが自然な発想です。
条件には $\angle\mathrm{POQ}=90^\circ$ というベクトルにおいて強力な条件があるので、ここから始めれば大丈夫です。

まとめ

今回は、大阪大学理系数学（2021年 第2問）の解説をしました。