東京大学 理系数学 2022年 第3問 解説

今回は、東京大学理系数学（2022年 第3問）の解説をしたいと思います。

問題

　$\mathrm{O}$ を原点とする座標平面上で考える。座標平面上の $2$ 点 $\mathrm{S}(x_1,y_1),$ $\mathrm{T}(x_2,y_2)$ に対し，点 $\mathrm{S}$ が点 $\mathrm{T}$ から十分離れているとは，
$$|x_1-x_2|\geqq 1 \quad \text{または} \quad |y_1-y_2|\geqq 1$$が成り立つことと定義する。
　不等式
$$0\leqq x\leqq 3,\quad 0\leqq y \leqq 3$$が表す正方形の領域を $D$ とし，その $2$ つの頂点 $\mathrm{A}(3,0),$ $\mathrm{B}(3,3)$ を考える。さらに，次の条件(ⅰ),(ⅱ)をともに満たす点 $\mathrm{P}$ をとる。
　(ⅰ) 点 $\mathrm{P}$ は領域 $D$ の点であり，かつ，放物線 $y=x^2$ 上にある。
　(ⅱ) 点 $\mathrm{P}$ は，$3$ 点 $\mathrm{O},\mathrm{A},\mathrm{B}$ のいずれからも十分離れている。
点 $\mathrm{P}$ の $x$ 座標を $a$ とする。

⑴　$a$ のとりうる値の範囲を求めよ。

⑵　次の条件(ⅲ),(ⅳ)をともに満たす点 $\mathrm{Q}$ が存在しうる範囲の面積 $f(a)$ を求めよ。
　(ⅲ) 点 $\mathrm{Q}$ は領域 $D$ の点である。
　(ⅳ) 点 $\mathrm{Q}$ は，$4$ 点 $\mathrm{O},\mathrm{A},\mathrm{B},\mathrm{P}$ のいずれからも十分離れている。

⑶　$a$ は⑴で求めた範囲を動くとする。⑵の $f(a)$ を最小にする $a$ の値を求めよ。

（東京大学）

解答

⑴

領域 $D$ 内で条件(ⅱ)をみたす部分は下図の網掛け部分である。ただし、境界線を含む。

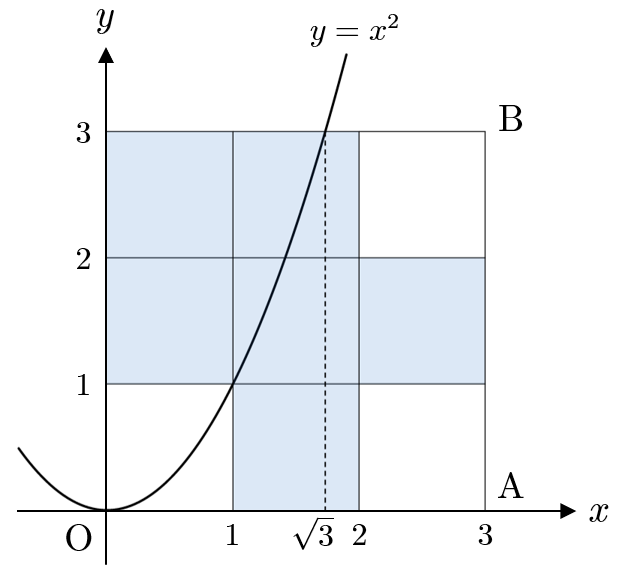
この領域と放物線 $y=x^2$ は放物線の $1\leqq x\leqq \sqrt{3}$ の部分で共有点をもつから、点 $\mathrm{P}$ が条件(ⅰ),(ⅱ)をともに満たす条件は $\boldsymbol{1\leqq a\leqq \sqrt{3}}$ である。

⑵

領域 $D$ 内で条件(ⅱ)をみたす部分の面積は、⑴の図より $6$ である。

そこから点 $\mathrm{P}$ を中心とする $1$ 辺の長さが $2$ の正方形の面積 $4$ を引き、引きすぎた部分の面積を足せば $f(a)$ となる。

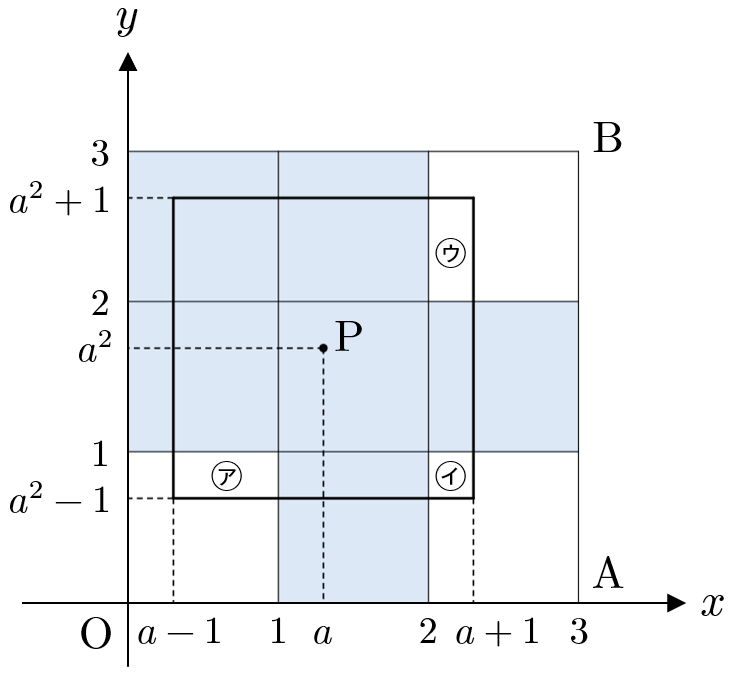
(ⅰ)　$1\leqq a\leqq \sqrt{2}$ のとき
下図より、引きすぎた部分は㋐,㋑,㋒の長方形の面積なので
$$\begin{eqnarray}
f(a) &=& 6-4+(2-a)(2-a^2)+(a-1)(2-a^2)+(a-1)(a^2-1) \\
&=& a^3-2a^2-a+5
\end{eqnarray}$$

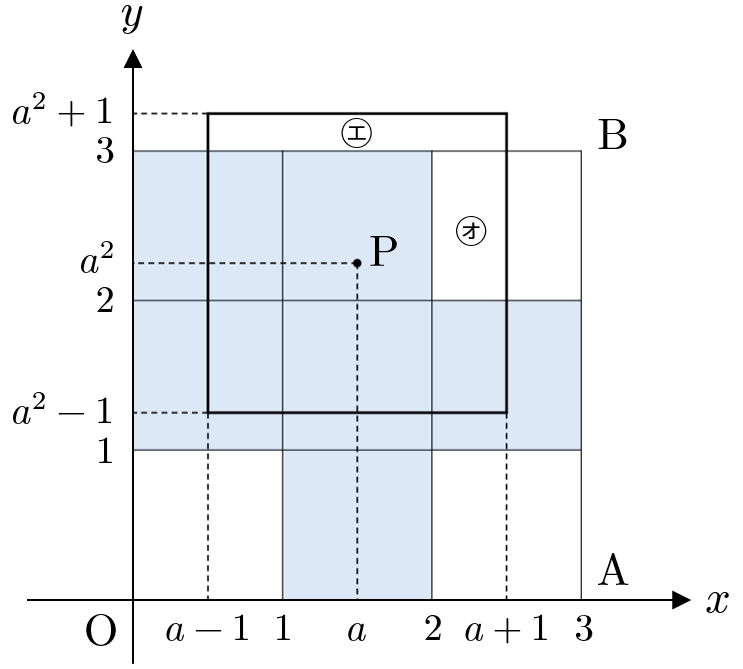
(ⅱ)　$\sqrt{2}\leqq a\leqq \sqrt{3}$ のとき
下図より、引きすぎた部分は㋓,㋔の長方形の面積なので
$$\begin{eqnarray}
f(a) &=& 6-4+2(a^2-2)+(a-1)\cdot 1 \\
&=& 2a^2+a-3
\end{eqnarray}$$

(ⅰ),(ⅱ)より、求める面積 $f(a)$ は
$$f(a)=
\begin{cases}
\boldsymbol{a^3-2a^2-a+5} & \mathbf{\text{（}} \ \boldsymbol{1\leqq a\leqq\sqrt{2}} \ \mathbf{\text{のとき）}} \\[0.3em]
\boldsymbol{2a^2+a-3} & \mathbf{\text{（}} \ \boldsymbol{\sqrt{2}\leqq a\leqq\sqrt{3}} \ \mathbf{\text{のとき）}}
\end{cases}$$

⑶

(ⅰ)　$1\leqq a\leqq \sqrt{2}$ のとき
$$f(a)=a^3-2a^2-a+5$$より
$$\begin{eqnarray}
f'(a) &=& 3a^2-4a-1=3\left(a-\dfrac{2}{3}\right)^2-\dfrac{7}{3} \\
&\leqq& 5-4\sqrt{2}=\sqrt{25}-\sqrt{32}\lt 0
\end{eqnarray}$$となるので $f(a)$ は単調減少であり、$a=\sqrt{2}$ で最小となる。

(ⅱ)　$\sqrt{2}\leqq a\leqq \sqrt{3}$ のとき
$$f(a)=2a^2+a-3$$より
$$f'(a)=4a+1\gt 0$$となるので $f(a)$ は単調増加であり、$a=\sqrt{2}$ で最小となる。

(ⅰ),(ⅱ)より、$f(a)$ を最小にする $a$ の値は $a=\boldsymbol{\sqrt{2}}$ である。

解説

図形や座標の問題を文章で説明する問題は長文になりがちなので、読み落としのないよう丁寧に読み進めることが重要です。

⑵は $a=\sqrt{2}$ を境目に $f(a)$ の求め方が変わることに注意しながら、効率よく面積を求めましょう。

ちなみに今回のように、場合分けの境目をどっちにいれるべきか悩む人もいるでしょうが、個人的には「どっちでもいい派」です。
つまり「 $1\leqq a\leqq \sqrt{2}$ と $\sqrt{2}\leqq a\leqq \sqrt{3}$ 」でも「 $1\leqq a\leqq \sqrt{2}$ と $\sqrt{2}\lt a\leqq \sqrt{3}$ 」でも「 $1\leqq a\lt \sqrt{2}$ と $\sqrt{2}\leqq a\leqq \sqrt{3}$ 」でも、どれでもいいと思います。本解答では1つめの表記をしていますが、この場合、境目で関数の値が連続であることが条件です。

まとめ

今回は、東京大学理系数学（2022年 第3問）の解説をしました。