今回は、東京大学理系数学(2021年 第1問)の解説をしたいと思います。
問題
$a,b$ を実数とする。座標平面上の放物線
$$C:\quad y=x^2+ax+b$$は放物線 $y=-x^2$ と $2$ つの共有点を持ち,一方の共有点の $x$ 座標は $-1\lt x\lt 0$ を満たし,他方の共有点の $x$ 座標は $0\lt x\lt 1$ を満たす。⑴ 点 $(a,b)$ のとりうる範囲を座標平面上に図示せよ。
⑵ 放物線 $C$ の通りうる範囲を座標平面上に図示せよ。
(東京大学)
解答
⑴
$y=x^2+ax+b$ と $y=-x^2$ から $y$ を消去すると
$$\begin{eqnarray}
x^2+ax+b &=& -x^2 \\
\therefore\quad 2x^2+ax+b &=& 0\quad\cdots\text{①}
\end{eqnarray}$$
①の解は $2$ つの放物線 $C$ と $y=-x^2$ の共有点の $x$ 座標を表すので、①の解が $-1\lt x\lt 0$ と $0\lt x\lt 1$ の範囲に $1$ つずつ存在するときに $a,b$ が満たすべき条件を考える。
①の左辺を $f(x)$ とおくと、①の解が $-1\lt x\lt 0$ と $0\lt x\lt 1$ の範囲に $1$ つずつ存在するのは
$$f(-1)\gt 0 \ \text{かつ} \ f(0)\lt 0 \ \text{かつ} \ f(1)\gt 0$$のときである。
$f(-1)\gt 0$ より
$$2-a+b \gt 0 \quad \Longleftrightarrow \quad b \gt a-2$$$f(0)\lt 0$ より
$$b \lt 0$$$f(1)\gt 0$ より
$$2+a+b \gt 0 \quad \Longleftrightarrow \quad b \gt -a-2$$
よって
$$b \gt a-2 \ \text{かつ} \ b \lt 0 \ \text{かつ} \ b \gt -a-2 \quad\cdots\text{②}$$
したがって、点 $(a,b)$ のとりうる範囲は下図の網掛け部分である。ただし、境界は含まない。
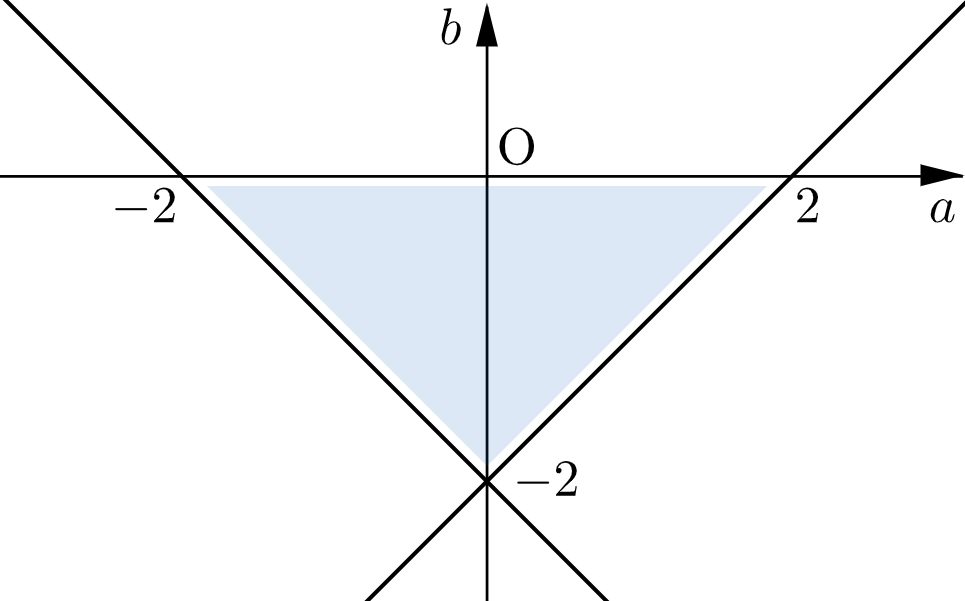
下図の網掛け部分(境界は含まない)

⑵
⑴で求めた点 $(a,b)$ の範囲を $D$ とする。
放物線 $C$ の通りうる範囲に点 $(X,Y)$ が含まれるとき、$Y=X^2+aX+b$ かつ②をみたすような実数 $a,b$ が存在する。
これは「 $ab$ 平面上において、直線 $b=-Xa+Y-X^2 \ \cdots\text{③}$ が領域 $D$ と共有点をもつ」$\cdots\text{④}$ ことと同値である。
領域 $D$ は $b$ 軸に関して対称である。
また
$$-Xa+Y-X^2=-\{-(-X)\}a+Y-\{-(-X)\}^2$$より、$2$ 直線 $b=-Xa+Y-X^2$ と $b=-(-X)a+Y-(-X)^2$ も $b$ 軸に関して対称である。
よって対称性より、直線③の傾きが $0$ 以上、すなわち $-X\geqq 0$ の場合のみを考えればよい。
ここで、③の右辺を $g(a)$ とおく。
(ⅰ) $0\leqq -X \leqq 1$ すなわち $-1\leqq X \leqq 0$ のとき
④が成り立つのは
$$g(-2)\lt0 \ \text{かつ} \ g(0)\gt -2$$のときである。
$g(-2) = 2X+Y-X^2\lt 0$ より
$$Y \lt X^2-2X \quad\cdots\text{⑤}
$$$g(0) = Y-X^2\gt -2$ より
$$Y \gt X^2-2 \quad\cdots\text{⑥}$$
⑤,⑥より
$$X^2-2 \lt Y \lt X^2-2X$$
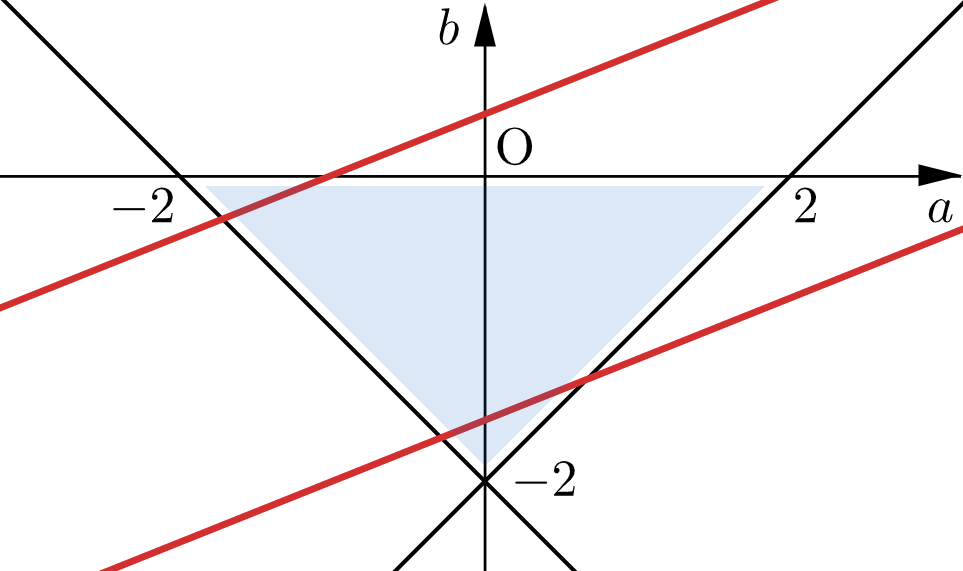
(ⅱ) $1\leqq -X$ すなわち $X\leqq -1$ のとき
④が成り立つのは
$$g(-2)\lt0 \ \text{かつ} \ g(2)\gt 0$$のときである。
$g(2) = -2X+Y-X^2 \gt 0$ より
$$Y \gt X^2+2X \quad\cdots\text{⑦}$$
⑤,⑦より
$$X^2+2X \lt Y \lt X^2-2X$$
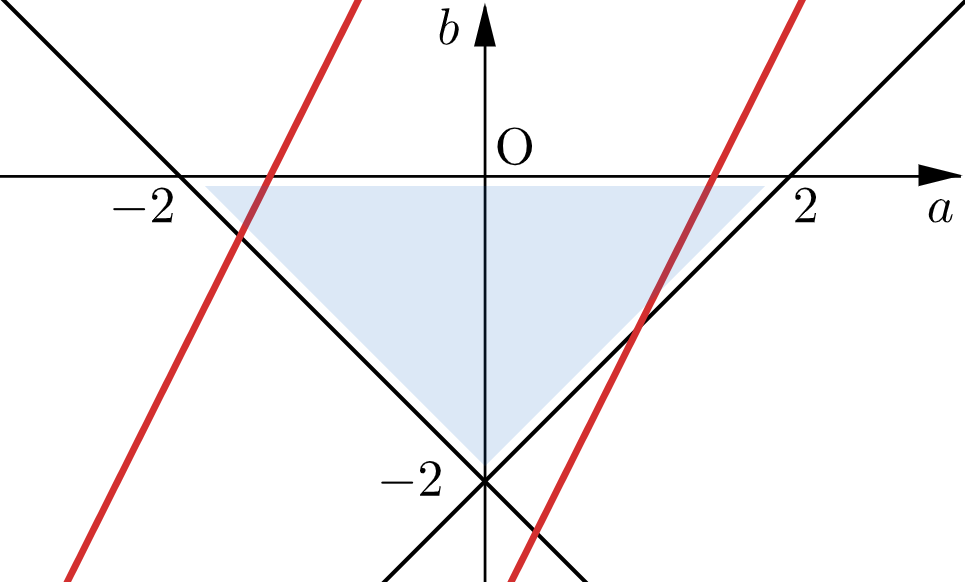
(ⅰ),(ⅱ)と対称性より、放物線 $C$ の通りうる範囲は下図の網掛け部分である。ただし、境界は含まない。
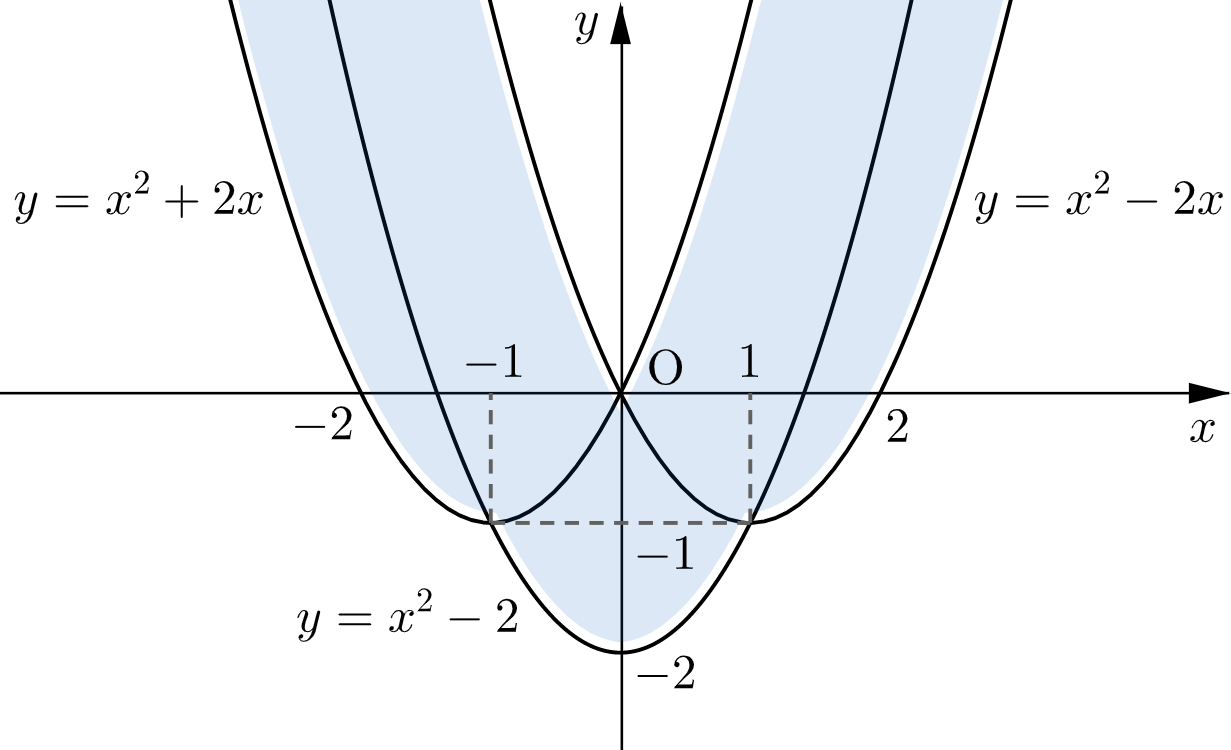
下図の網掛け部分(境界は含まない)

解説
⑴は練習問題などで解いたことがある人もいると思いますが、今一度何をやっているのか確認しましょう。
曲線の方程式が $2$ つあるからなんとなく $y$ を消去していませんか?求まった解 $x$ は $2$ 曲線の交点の $x$ 座標を表しています。
$2$ 次方程式の解の配置問題、なんとなく条件を与えていませんか?その条件が本当に必要十分条件になっているのか、放物線の軸や開き具合をいろいろ考えて、過不足のないように注意しましょう。
⑵は苦手とする人も多い「通過領域」の問題です。実は私も苦手です(笑)。
今回は⑴で点 $(a,b)$ の存在範囲を図示したので、流れに乗って「逆像法」により求めました。つまり「ある点 $(X,Y)$ が $C$ の通過領域に属するならば、$Y=X^2+aX+b$ をみたすような実数 $a,b$ の組 $(a,b)$ が⑴の範囲内に存在する」という方法ですね。
通過領域の問題は「順像法」と「逆像法」どちらでも解ける問題が多いので、両方で解けるようにしておくと安心かもしれません。
まとめ
今回は、東京大学理系数学(2021年 第1問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2021年 第1問 解説
東京大学 理系数学 2021年 第2問 解説
東京大学 理系数学 2021年 第3問 解説
東京大学 理系数学 2021年 第4問 解説
東京大学 理系数学 2021年 第5問 解説
東京大学 理系数学 2021年 第6問 解説













