京都大学 理学部特色入試（数学）2021年度 第2問 解説

今回は、京都大学理学部特色入試・数学（2021年度 第2問）の解説をしたいと思います。

問題

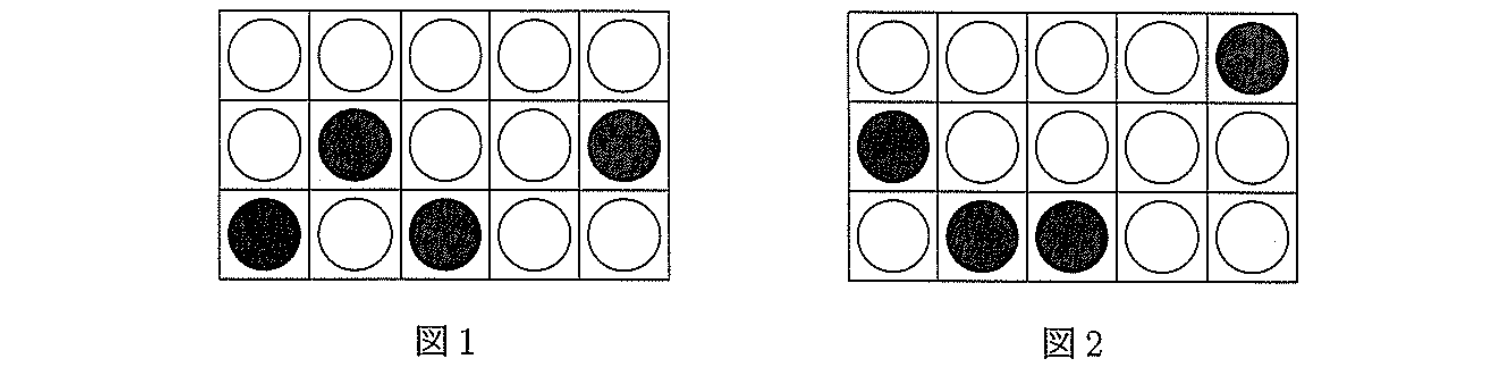
　自然数 $n,m$ に対して横 $n$ 個，縦 $m$ 個からなる $n\times m$ 個のマスを考え，それぞれのマスに $1$ つずつ白玉または黒玉を入れる．その白玉と黒玉の入れ方のうち，黒玉が上下左右いずれにも隣り合わないような入れ方の総数を $a_{n,m}$ とする．例えば $n=5, \ $$m=3$ のとき，図 $1$ の入れ方は黒玉が上下左右いずれにも隣り合わないような入れ方であり，図 $2$ の入れ方は黒玉が左右に隣り合っている入れ方である．

以下の設問に答えよ．

⑴　$a_{n,2}$ を求めよ．

⑵　ある正の実数 $D$ が存在して，すべての自然数 $n$ について
$$\dfrac{1}{2}\leqq\dfrac{\log_{2}a_{n,n}}{n^2}\leqq\dfrac{1}{2}\log_{2}(1+\sqrt{2})+\dfrac{D}{n}$$となることを示せ．

（京都大学）

解答

⑴

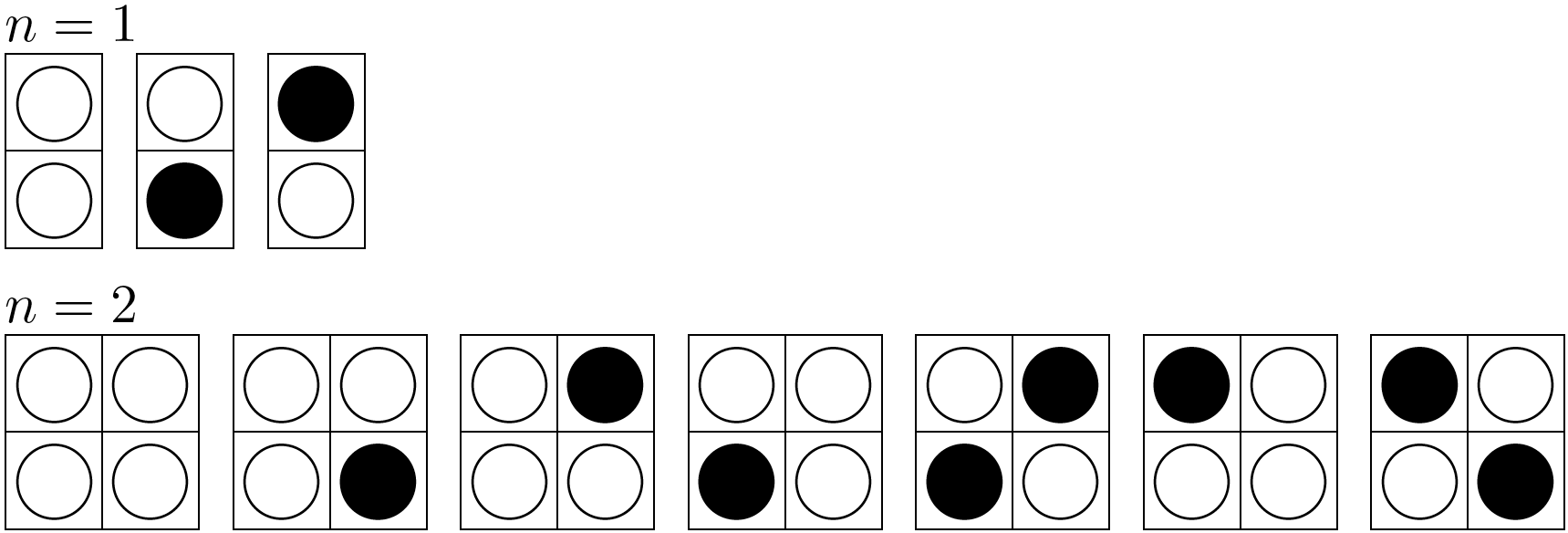
$a_{n,2}$ のうち、最も右側の列が $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ であるものの総数を $p_n$ ，$\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{●}} \\ \hline \end{array}$ または $\begin{array}{|c|} \hline {\large\text{●}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ であるものの総数を $q_n$ とする。

$p_1=1, \ $$p_2=3$ である。

$(n+1)\times 2$ 個のマスの最も右側の列が $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ のとき、右から $2$ 列目は $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ または $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{●}} \\ \hline \end{array}$ または $\begin{array}{|c|} \hline {\large\text{●}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ となる。また、最も右側の列が $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{●}} \\ \hline \end{array}$$\left(\begin{array}{|c|} \hline {\large\text{●}} \\ \hline {\large\text{○}} \\ \hline \end{array}\right)$ のとき、右から $2$ 列目は $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ または $\begin{array}{|c|} \hline {\large\text{●}} \\ \hline {\large\text{○}} \\ \hline \end{array}$$\left(\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{●}} \\ \hline \end{array}\right)$ となる。

したがって
$$\left\{
\begin{align}
p_{n+1} &= p_n+q_n \\
q_{n+1} &= 2p_n+q_n
\end{align}
\right.$$が成り立つ（補足1）。

よって
$$\begin{align}
p_{n+2} &= p_{n+1}+q_{n+1} \\
&= p_{n+1}+2p_n+q_n \\
&= p_{n+1}+2p_n+(p_{n+1}-p_n) \\[0.3em]
\therefore \ p_{n+2}&= 2p_{n+1}+p_n
\end{align}$$

$\alpha=1-\sqrt{2}, \ $$\beta=1+\sqrt{2}$ とすると（補足2）
$$\left\{
\begin{alignat}{2}
p_{n+2}-\alpha p_{n+1} &= \beta(p_{n+1}-\alpha p_n)& &\quad\cdots\text{①} \\
p_{n+2}-\beta p_{n+1} &= \alpha(p_{n+1}-\beta p_n)& &\quad\cdots\text{②}
\end{alignat}
\right.$$①より
$$\begin{align}
p_{n+1}-\alpha p_{n} &= \beta^{n-1}(p_2-\alpha p_1) \\
&= \beta^{n-1}(3-\alpha) \\
&= \beta^{n-1}\cdot\sqrt{2}\beta \\[0.3em]
\therefore \ p_{n+1}-\alpha p_{n} &= \sqrt{2}\beta^n \quad\cdots\text{③}
\end{align}$$②より
$$\begin{align}
p_{n+1}-\beta p_{n} &= \alpha^{n-1}(p_2-\beta p_1) \\
&= \alpha^{n-1}(3-\beta) \\
&= \alpha^{n-1}\cdot(-\sqrt{2}\alpha) \\[0.3em]
\therefore \ p_{n+1}-\beta p_{n} &= -\sqrt{2}\alpha^n \quad\cdots\text{④}
\end{align}$$③$-$④より
$$\begin{align}
(\beta-\alpha)p_n&=\sqrt{2}(\alpha^n+\beta^n) \\
\therefore \ p_n&=\dfrac{1}{2}(\alpha^n+\beta^n)
\end{align}$$

したがって
$$\begin{align}
a_{n,2} &= p_n+q_n \\
&= p_{n+1} \\
&= \dfrac{1}{2}(\alpha^{n+1}+\beta^{n+1}) \\
&= \boldsymbol{\dfrac{1}{2}\{(1-\sqrt{2})^{n+1}+(1+\sqrt{2})^{n+1}\}}
\end{align}$$

⑵

示すべき不等式は
$$\left\{
\begin{alignat}{2}
&\dfrac{1}{2}\leqq\dfrac{\log_{2}a_{n,n}}{n^2}& &\quad\cdots\text{⑤} \\
&\dfrac{\log_{2}a_{n,n}}{n^2}\leqq\dfrac{1}{2}\log_{2}(1+\sqrt{2})+\dfrac{D}{n}& &\quad\cdots\text{⑥}
\end{alignat}
\right.$$と同値である。

(ⅰ)　⑤が成り立つことの証明

下図のように、$n\times n$ 個のマスの左上を「×」とし、○と×が交互に並ぶように配置する。

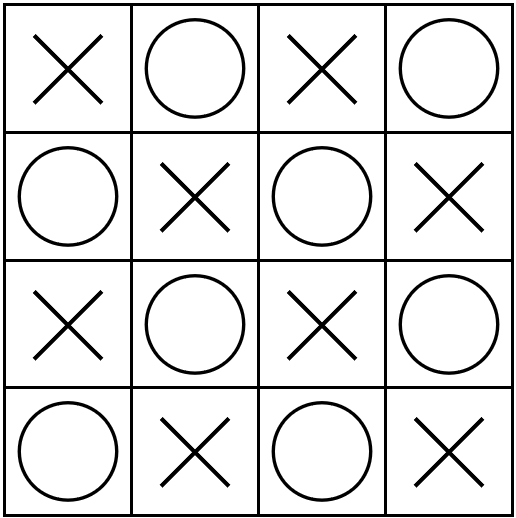
このとき、×は上下左右いずれにも隣り合わないので、×の位置には○または●を自由に選択して入れることができる。

$n$ が偶数のとき、×は $n\times n$ 個のマスの半分、すなわち $\dfrac{n^2}{2}$ 個ある。$n$ が奇数のとき、×は○より $1$ 個だけ多く、全部で $\dfrac{n^2+1}{2}$ 個ある。いずれにせよ、×は $\dfrac{n^2}{2}$ 個以上あるので
$$a_{n,n} \geqq 2^{\frac{n^2}{2}}$$が成り立つ。両辺に対して $2$（ $\gt 1$ ）を底とする対数をとると
$$\begin{align}
\log_2 a_{n,n} &\geqq \dfrac{n^2}{2} \\
\therefore \ \dfrac{1}{2} &\leqq \dfrac{\log_{2}a_{n,n}}{n^2}
\end{align}$$

したがって、すべての自然数 $n$ について⑤が成り立つ。

(ⅱ)　⑥が成り立つことの証明

$n\times n$ 個のマスを、上から $2$ 行ずつのブロックに分ける。ただし、$n$ が奇数のときは $(n+1)$ 行目に「すべてが○である行」を追加し、$n\times(n+1)$ 個のマスとして考える。

この $2$ 行ごとのブロックは、$n$ が偶数ならば $\dfrac{n}{2}$ 個でき、$n$ が奇数ならば $\dfrac{n+1}{2}$ 個できる。いずれにせよ、ブロックの数は $\dfrac{n+1}{2}$ 個以下である。

$n\times n$ 個（あるいは $n\times(n+1)$ 個）のマスにおいて黒玉が上下左右いずれにも隣り合わないとき、それぞれのブロックにおいても同様に条件を満たす。

よって
$$a_{n,n} \leqq (a_{n,2})^{\frac{n+1}{2}}$$が成り立つ。両辺に対して $2$（ $\gt 1$ ）を底とする対数をとると
$$\begin{align}
\log_2 a_{n,n} &\leqq \dfrac{n+1}{2}\log_2 a_{n,2} \\
&= \dfrac{n+1}{2}\log_2 \left\{\dfrac{1}{2}(\alpha^{n+1}+\beta^{n+1})\right\} \\
&\leqq \dfrac{n+1}{2}\log_2 \left\{\dfrac{1}{2}(\beta^{n+1}+\beta^{n+1})\right\} \ \text{（}\because |\alpha|\lt\beta \ \text{）} \\
&= \dfrac{n+1}{2}\log_2 \beta^{n+1} \\
&= \dfrac{(n+1)^2}{2}\log_2 (1+\sqrt{2}) \\
&= \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + \left(n+\dfrac{1}{2}\right)\log_2 (1+\sqrt{2}) \\
&\leqq \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + (n+n)\log_2 (1+3) \\
&= \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + 4n
\end{align}$$両辺を $n^2$（ $\gt 0$ ）で除すと
$$\dfrac{\log_{2}a_{n,n}}{n^2}\leqq\dfrac{1}{2}\log_{2}(1+\sqrt{2})+\dfrac{4}{n}$$となり、$D=4$ とすれば⑥が成り立つ。

(ⅰ),(ⅱ)より、$D=4$ のとき、すべての自然数 $n$ について与不等式が成り立つ。$$\tag{証明終}$$

別解

※ (ⅱ) ⑥の証明の別解です。

下図のように、$n\times(m+2)$ 個のマスを「 $n\times m$ 個のマス」「 $n\times 2$ 個のマス」の $2$ ブロックに分ける。

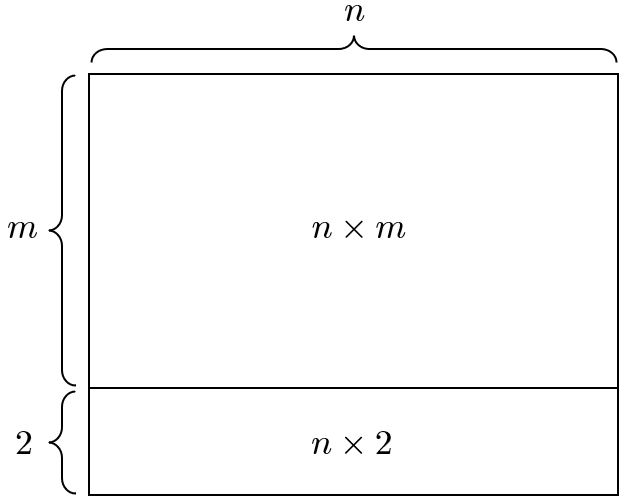
$n\times(m+2)$ 個のマスにおいて黒玉が上下左右いずれにも隣り合わないとき、これら $2$ ブロックそれぞれにおいても同様に条件を満たす。

よって
$$a_{n,m+2} \leqq a_{n,m} \cdot a_{n,2}$$が成り立ち、両辺に対して $2$（ $\gt 1$ ）を底とする対数をとると
$$\log_2 a_{n,m+2} \leqq \log_2 a_{n,m} + \log_2 a_{n,2}$$となる。

(ア)　$n$ が偶数のとき
$n=2k$（ $k$ は $1$ 以上の整数）とおくと、$k\geqq 2$ のとき
$$\begin{align}
\log_2 a_{2k,2k} &\leqq \log_2 a_{2k,2k-2} + \log_2 a_{2k,2} \\
&\leqq (\log_2 a_{2k,2k-4} + \log_2 a_{2k,2}) + \log_2 a_{2k,2} \\
&\leqq \cdots \\
&\leqq \log_2 a_{2k,2} + (k-1)\log_2 a_{2k,2} \\
&= k\log_2 a_{2k,2}
\end{align}$$となる。これは $k=1$ のときも成り立つ。

したがって、⑴の結果と $k=\dfrac{n}{2}, \ $$\beta=1+\sqrt{2}$ より
$$\begin{align}
\log_2 a_{n,n} &\leqq \dfrac{n}{2}\log_2 \left\{\dfrac{1}{2}(\alpha^{n+1}+\beta^{n+1})\right\} \\
&\leqq \dfrac{n}{2}\log_2 \left\{\dfrac{1}{2}(\beta^{n+1}+\beta^{n+1})\right\} \ \text{（}\because |\alpha|\lt\beta \ \text{）} \\
&= \dfrac{n}{2}(n+1)\log_2 (1+\sqrt{2}) \\
&\leqq \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + \dfrac{n}{2}\log_2 (1+3) \\
&= \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + n
\end{align}$$となる。両辺を $n^2$（ $\gt 0$ ）で除すと
$$\dfrac{\log_{2}a_{n,n}}{n^2}\leqq\dfrac{1}{2}\log_{2}(1+\sqrt{2})+\dfrac{1}{n}$$となり、$D\geqq 1$ のとき⑥が成り立つ。

(イ)　$n$ が奇数のとき
$n=2k-1$（ $k$ は $1$ 以上の整数）とおくと、$k\geqq 2$ のとき、(ア)と同様に
$$\begin{align}
\log_2 a_{2k-1,2k-1} &\leqq \log_2 a_{2k-1,1}+(k-1)\log_2 a_{2k-1,2} \\
&\leqq k\log_2 a_{2k-1,2} \ \text{（}\because a_{2k-1,1}\leqq a_{2k-1,2} \ \text{）}
\end{align}$$となる。これは $k=1$ のときも成り立つ。

したがって、⑴の結果と $k=\dfrac{n+1}{2}, \ $$\beta=1+\sqrt{2}$ より
$$\begin{align}
\log_2 a_{n,n} &\leqq \dfrac{n+1}{2}\log_2 \left\{\dfrac{1}{2}(\alpha^{n+1}+\beta^{n+1})\right\} \\
&\leqq \dfrac{n+1}{2}\log_2 \left\{\dfrac{1}{2}(\beta^{n+1}+\beta^{n+1})\right\} \ \text{（}\because |\alpha|\lt\beta \ \text{）} \\
&= \dfrac{(n+1)^2}{2}\log_2 (1+\sqrt{2}) \\
&\leqq \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + \left(n+\dfrac{1}{2}\right)\log_2 (1+\sqrt{2}) \\
&\leqq \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + (n+n)\log_2 (1+3) \\
&= \dfrac{n^2}{2}\log_2 (1+\sqrt{2}) + 4n
\end{align}$$となる。両辺を $n^2$（ $\gt 0$ ）で除すと
$$\dfrac{\log_{2}a_{n,n}}{n^2}\leqq\dfrac{1}{2}\log_{2}(1+\sqrt{2})+\dfrac{4}{n}$$となり、$D\geqq 4$ のとき⑥が成り立つ。

(ア),(イ)より、$D=4$ とすれば、すべての自然数 $n$ について⑥が成り立つ。

解説

⑴は、黒玉が隣り合わないという制約がついており、直接求めることが難しそうなので、漸化式を立てるという発想になります。
$$\left\{
\begin{align}
p_{n+1} &= p_n+q_n \\
q_{n+1} &= 2p_n+q_n
\end{align}
\right.$$から $p_{n+2}$ は若干見えにくいですが、何とか取りたい問題です。

⑵は、まず処理しやすそうな左辺を示していきます。$n^2$ や $\log_2$ を移行すれば、$a_{n,n} \geqq 2^{\frac{n^2}{2}}$ となって「 $n\times n$ 個のマスの半分」がからんでいることがわかります。市松模様状に○と×を並べるという発想が思いつくかどうかがカギです。

右辺を示す上でまず注目するのが $1+\sqrt{2}$ という微妙な数です。どこからこの数が出てくるのかと考えると、$a_{n,2}$ の中に登場するのが分かります。また、$\alpha=1-\sqrt{2}$ が出てこないのは、累乗する中で $\alpha\lt\beta$ が効いてくるからかなと推測できます。

$a_{n,2}$ が関係してくるということから、全体のマス目を $2$ 行ごとに区切るとどうなるかという考え方にたどり着けるかどうかが山場だと思います。

また別解のように、全体のマス目に $2$ 行を追加して漸化式をつくり、それを繰り返し使って $a_{2k,2}$（ $a_{2k-1,1}$ ）まで下げる考え方もありますが、最初から $2$ 行ごとに分けておく方が解答としてはシンプルになります。

補足

〔1〕
$$q_{n+1} = 2p_n+q_n$$の $p_n$ の係数が $2$ なのは、最も右側の列が $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ である $n\times 2$ 個のマス $1$ パターンに対して、$(n+1)$ 列目としては $\begin{array}{|c|} \hline {\large\text{○}} \\ \hline {\Large\text{●}} \\ \hline \end{array}$ または $\begin{array}{|c|} \hline {\Large\text{●}} \\ \hline {\large\text{○}} \\ \hline \end{array}$ の $2$ パターンがあるためです。
（解答へ戻る）

〔2〕
$\alpha,\beta$ は特性方程式 $c^2-2c-1=0$ の解です。
（解答へ戻る）

まとめ

今回は、京都大学理学部特色入試・数学（2021年度 第2問）の解説をしました。