京都大学 理系数学 2019年 第5問 解説

今回は、京都大学理系数学（2019年 第5問）の解説をしたいと思います。

問題

　半径 $1$ の球面上の $5$ 点 $\mathrm{A},\,$$\mathrm{B}_1,\,$$\mathrm{B}_2,\,$$\mathrm{B}_3,\,$$\mathrm{B}_4$ は，正方形 $\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ を底面とする四角錐をなしている。この $5$ 点が球面上を動くとき，四角錐 $\mathrm{A}\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ の体積の最大値を求めよ。

（京都大学）

解答

半径 $1$ の球面の中心を $\mathrm{O}$，正方形 $\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ の対角線の交点を $\mathrm{C}$ とする。

正方形 $\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ を固定して考えると、四角錐 $\mathrm{A}\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ の体積が最大となるのは、半直線 $\mathrm{CO}$ と球面の交点に $\mathrm{A}$ があるときである。

なお、$\mathrm{C}$ と $\mathrm{O}$ が一致する場合は、$\mathrm{C}$ を通り正方形 $\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ に垂直な直線と球面の交点のいずれかに $\mathrm{A}$ があるときである。

このように点 $\mathrm{A}$ を定めたとき、$\mathrm{AC}=h$ とおく。

点 $\mathrm{A}$ の定め方より、$h$ のとりうる範囲は $1\leqq h\lt2$ である。

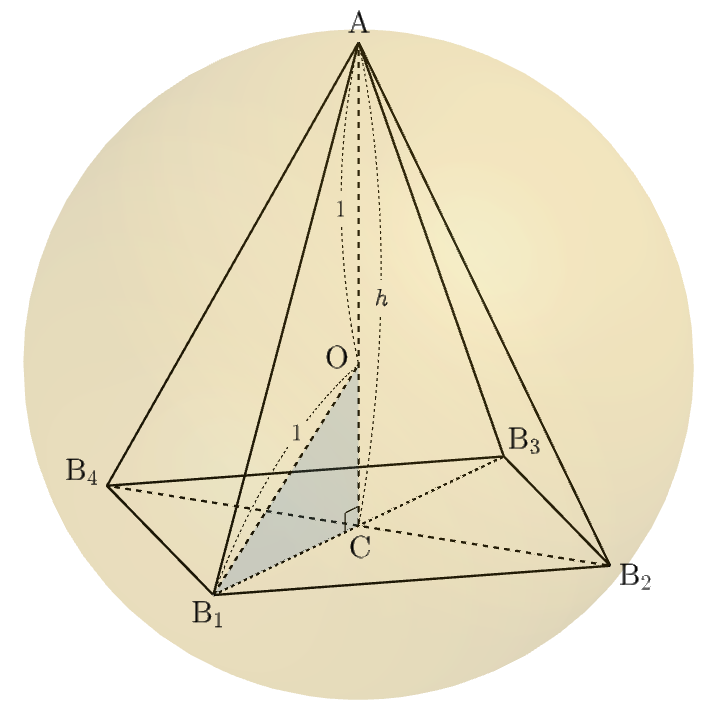
$\mathrm{OB}_1=1$，$\mathrm{OC}=h-1$ より
$$\mathrm{B}_1\mathrm{C}=\sqrt{1^2-(h-1)^2}=\sqrt{2h-h^2}$$となる。

よって、四角錐 $\mathrm{A}\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ の体積を $V(h)$ とすると
$$\begin{align}
V(h) &= \dfrac{1}{3}\cdot\left(\sqrt{2\vphantom{2h-h^2}}\sqrt{2h-h^2}\right)^2\cdot h \\
&= \dfrac{2}{3}(2h^2-h^3)
\end{align}$$となる。

$$V'(h)=\dfrac{2}{3}(4h-3h^2)=\dfrac{2}{3}h(4-3h)$$より、$1\leqq h\lt2$ における $V$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c}\hline
h & 1 & \cdots & \dfrac{4}{3} & \cdots & (2) \\ \hline
V'(h) & & + & 0 & – & \\ \hline
V & & \nearrow & \text{最大} & \searrow & \\ \hline
\end{array}$$

したがって、$V(h)$ は $h=\dfrac{4}{3}$ のとき最大となり、その最大値は
$$\begin{align}
V\left(\dfrac{4}{3}\right) &= \dfrac{2}{3}\cdot\left(\dfrac{4}{3}\right)^2\cdot\left(2-\dfrac{4}{3}\right) \\
&= \boldsymbol{\dfrac{64}{81}}
\end{align}$$

解説

まず問題文の設定として、点 $\mathrm{A}$ が正方形 $\mathrm{B}_1\mathrm{B}_2\mathrm{B}_3\mathrm{B}_4$ の中心（$\,\mathrm{C}\,$）の真上にあるとは限らないことに注意しましょう。

四角錐の体積が最大になるときの $5$ 点の位置について説明したら、次は体積計算です。

高さ関係（$\,\mathrm{AC}$ や $\mathrm{OC}\,$）か正方形関係（$\,\mathrm{B}_1\mathrm{C}$ や $\mathrm{B}_1\mathrm{B}_2\,$）のどちらかを変数にとることになりますが、後者の場合、$V$ の式に $\sqrt{\vphantom{a}\hphantom{=}}$ が入って計算が煩雑になるので、前者を選んで計算ミスを減らしましょう。

ちなみに、$V(h)$ が最大のとき、球に占める充填率を計算してみると
$$\dfrac{64}{81}\div\dfrac{4\pi}{3}\fallingdotseq\mathscr{18.9}\,\%$$となり、$5$ 分の $1$ にも満たないことが分かります。

まとめ

今回は、京都大学理系数学（2019年 第5問）の解説をしました。