一橋大学 数学 2021年[後期] 第1問 解説

今回は、一橋大学数学（2021年後期 第1問）の解説をしたいと思います。

問題

　方程式
$$(\sin x+1)(\cos x+1)=k$$の解が $0\leqq x\lt2\pi$ の範囲にちょうど $2$ つあるような実数 $k$ を求めよ。

（一橋大学）

解答

解法1（数Ⅲ使わず）

与式より
$$\sin x\cos x+\sin x+\cos x+1=k \quad\cdots\text{①}$$

$\sin x+\cos x=t \ \quad\cdots\text{②}$ とおくと
$$t=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)\quad(0\leqq x\lt2\pi) \quad\cdots\text{③}$$より $-\sqrt{2}\leqq t\leqq\sqrt{2} \ \quad\cdots\text{④}$ である。

また、②の両辺を $2$ 乗すると
$$\begin{array}{c}
\sin^2x+2\sin x\cos x+\cos^2x=t^2 \\[0.2em]
\therefore \ \sin x\cos x=\dfrac{t^2-1}{2} \quad\cdots\text{⑤}
\end{array}$$

②,⑤を①に代入すると
$$\begin{align}
\dfrac{t^2-1}{2}+t+1 &= k \\
\therefore \ \dfrac{1}{2}(t+1)^2 &= k \quad\cdots\text{⑥}
\end{align}$$

よって、①の解の個数は、⑥の解 $t$ に対する③の解の個数に等しい。

ここで、$y=\dfrac{1}{2}(t+1)^2$ および③のグラフは下図のようになる。

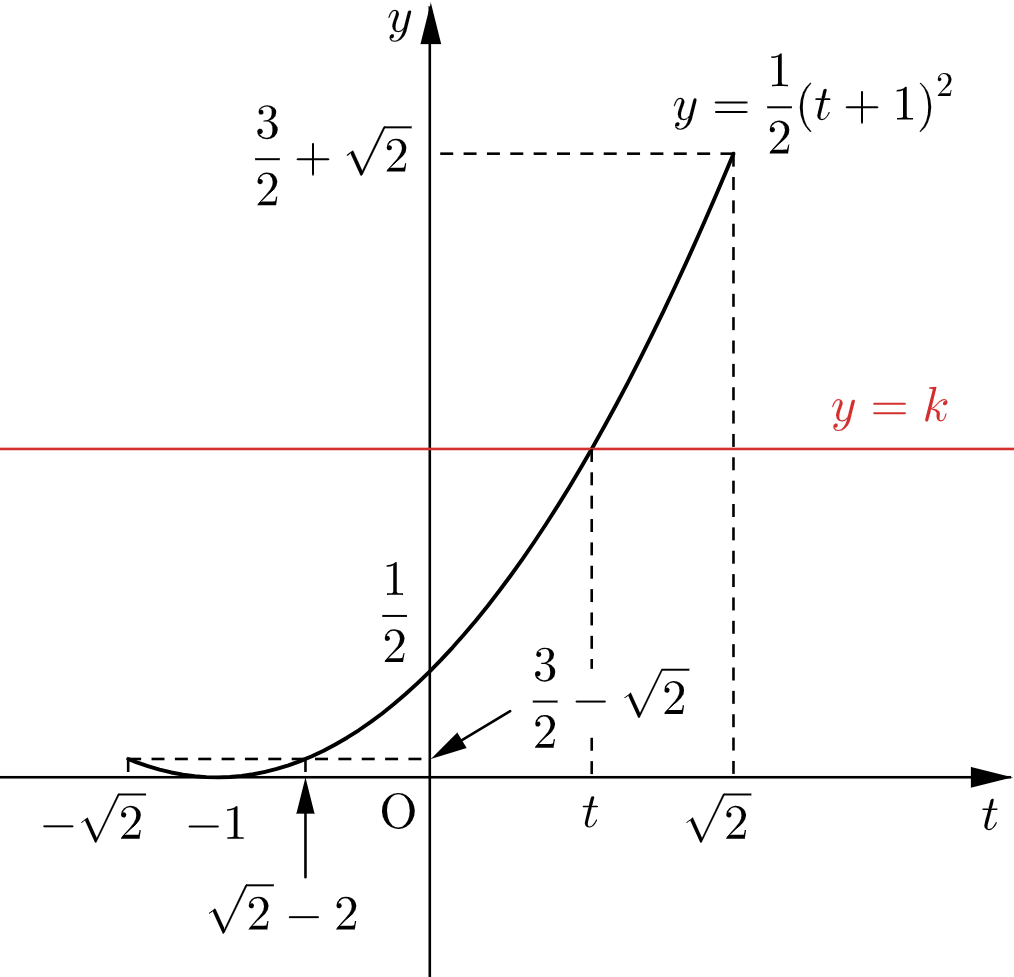
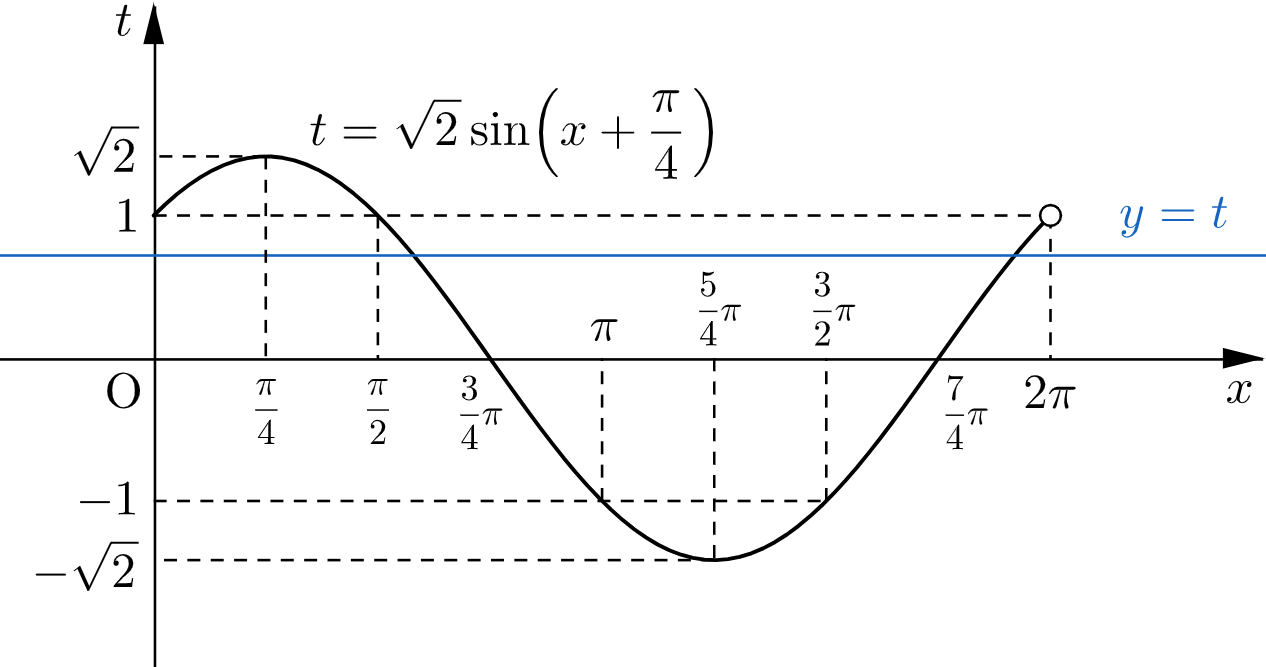
(ⅰ)　$k\lt0$，$\dfrac{3}{2}+\sqrt{2}\lt k$ のとき
⑥の解は存在しないので、③の解も存在せず不適。

(ⅱ)　$k=0$ のとき
⑥の解は $t=-1$ なので、③の解は $2$ つである。

(ⅲ)　$0\lt k\lt\dfrac{3}{2}-\sqrt{2}$ のとき
⑥の解は $-\sqrt{2}\lt t\lt-1$，$-1\lt t\lt\sqrt{2}-2$ の範囲に $1$ つずつ存在するので、③の解は $4$ つである。

(ⅳ)　$k=\dfrac{3}{2}-\sqrt{2}$ のとき
⑥の解は $t=-\sqrt{2}, \ \sqrt{2}-2$ なので、③の解は $3$ つである。

(ⅴ)　$\dfrac{3}{2}-\sqrt{2}\lt k\leqq\dfrac{3}{2}+\sqrt{2}$ のとき
⑥の解は $\sqrt{2}-2\lt t\leqq\sqrt{2}$ の範囲に $1$ つ存在するので、③の解は $2$ つである。

(ⅰ)～(ⅴ)より、求める $k$ は
$$\boldsymbol{k=0}, \ \ \boldsymbol{\dfrac{3}{2}-\sqrt{2}\lt k\leqq\dfrac{3}{2}+\sqrt{2}}$$

解法2（数Ⅲ使って）

与式の左辺を $f(x)$ とおくと
$$\begin{align}
f'(x) &= \cos x(\cos x+1)+(\sin x+1)(-\sin x) \\
&= \cos^2x-\sin^2x+\cos x-\sin x \\[0.2em]
&= (\cos x-\sin x)(\cos x+\sin x+1) \\[0.3em]
&= \left\{\sqrt{2}\cos\left(x+\dfrac{\pi}{4}\right)\right\}\left\{\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)+1\right\}
\end{align}$$より
$$\begin{alignat}{2}
f'(x)=0 \ &\Longleftrightarrow& \ \ x+\dfrac{\pi}{4}&=\dfrac{\pi}{2},\,\dfrac{5}{4}\pi,\,\dfrac{3}{2}\pi,\,\dfrac{7}{4}\pi \\[0.3em]
&\Longleftrightarrow& x&=\dfrac{\pi}{4},\,\pi,\,\dfrac{5}{4}\pi,\,\dfrac{3}{2}\pi
\end{alignat}$$となるので、$0\leqq x\lt2\pi$ における $f(x)$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c} \hline
x & 0 & \cdots & \dfrac{\pi}{4} & \cdots & \pi & \cdots & \dfrac{5}{4}\pi & \cdots & \dfrac{3}{2}\pi & \cdots & (2\pi) \\ \hline
f'(x) & & + & 0 & – & 0 & + & 0 & – & 0 & + & \\ \hline
f'(x) & 2 & \nearrow & \dfrac{3}{2}+\sqrt{2} & \searrow & 0 & \nearrow & \dfrac{3}{2}-\sqrt{2} & \searrow & 0 & \nearrow & (2) \\ \hline
\end{array}$$

増減表より、$y=f(x)$ のグラフは下図のようになる。

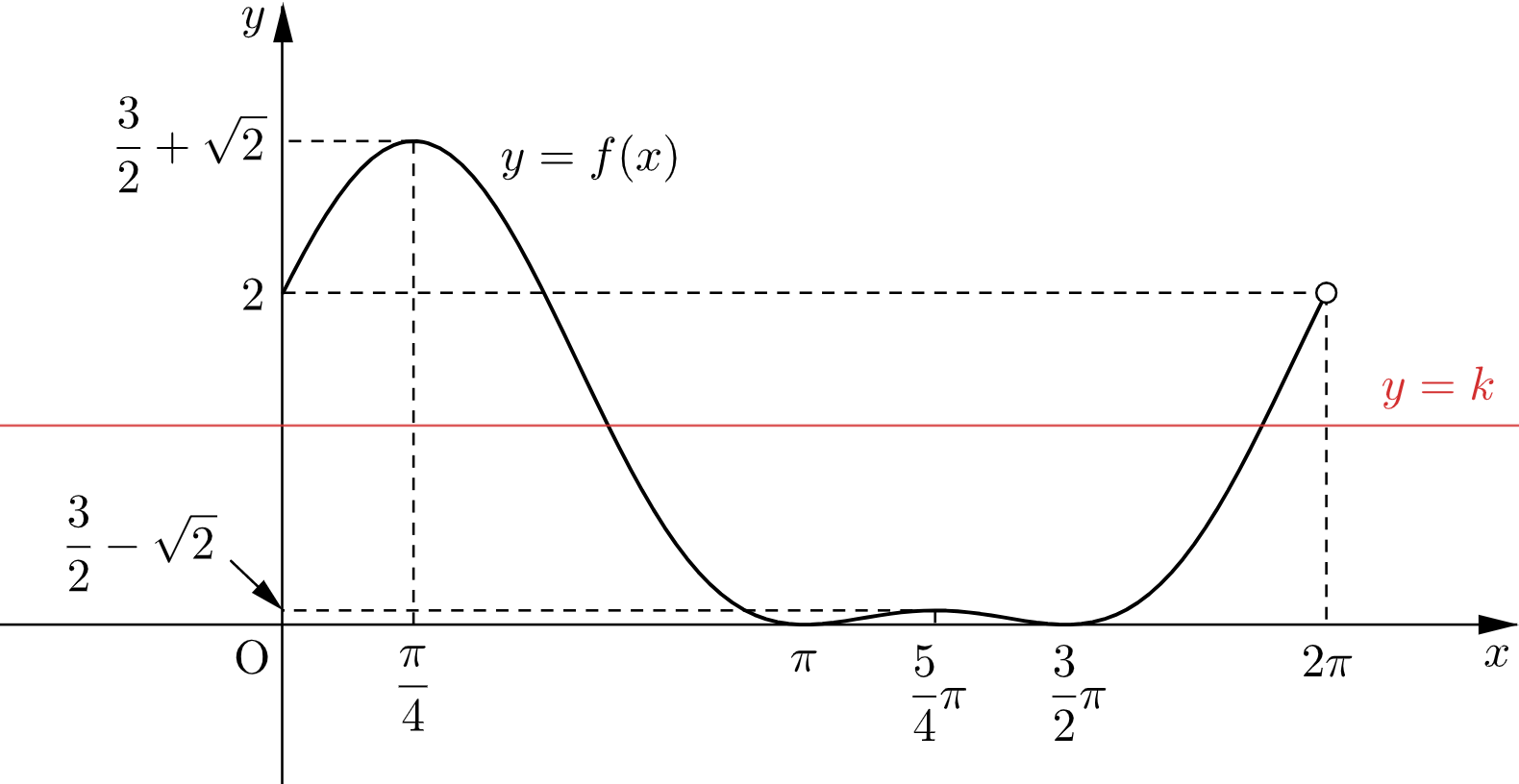
与式の解の個数は $y=f(x)$ と $y=k$ の共有点の個数に等しいので、求める $k$ は
$$\boldsymbol{k=0}, \ \ \boldsymbol{\dfrac{3}{2}-\sqrt{2}\lt k\leqq\dfrac{3}{2}+\sqrt{2}}$$

解説

大学側の想定解は数Ⅲを使わない「解法1」ですが、$\sin x+\cos x=t$ の置換が思いつきにくいかもしれません。

また、$k$ の値に応じて⑥の解 $t$ の個数が変わり、それによって③の解 $x$ の個数が変わる、という風に $2$ 段階の変化を考えなければならないところがポイントです。

ちなみに $k=2$ では、$x$ の定義域に $2\pi$ が入っていないことから実数解 $x$ は $2$ つとなり答えに含まれることに（$\,3$ つと勘違いして答えから除外しないように）注意しましょう。

一方、数Ⅲが使える人にとっては、「解法2」の方が思いつきやすかったかもしれません。

増減表は大きくなりますが、答えまで $1$ 本道なので計算ミスにさえ気を付ければ大丈夫です。

まとめ

今回は、一橋大学数学（2021年後期 第1問）の解説をしました。