今回は、京都大学理学部特色入試・数学(2021年度 第4問)の解説をしたいと思います。
問題
$C$ を $1$ 以上の実数,$\{a_n\}$ を $0$ 以上の整数からなる数列で $a_1=0, \ $$a_2=1$ を満たすとする.$xy$ 平面上の点 $\mathrm{A}_n=(a_n,a_{n+1})$ はすべての $n=1,2,3,\dots$ について次の条件(ⅰ),(ⅱ),(ⅲ)を満たすとする.
(ⅰ) $3$ 点 $\mathrm{A}_n,\mathrm{O},\mathrm{A}_{n+1}$ は同一直線上になく,三角形 $\mathrm{A}_n\mathrm{OA}_{n+1}$ と三角形 $\mathrm{A}_{n+1}\mathrm{OA}_{n+2}$ の内部は互いに交わらない.
(ⅱ) 三角形 $\mathrm{A}_n\mathrm{OA}_{n+1}$ の面積は $C$ より小さい.
(ⅲ) $\angle\mathrm{A}_1\mathrm{OA}_{n+1}\lt\dfrac{\pi}{4}$ かつ $\displaystyle\lim_{n\to\infty}\angle\mathrm{A}_1\mathrm{OA}_{n+1}=\dfrac{\pi}{4}$ である.
ここで $\mathrm{O}$ は $xy$ 平面の原点を表す.以下の設問に答えよ.
⑴ $C=100$ のとき,(ⅰ),(ⅱ),(ⅲ)を満たす数列 $\{a_n\}$ の例を $1$ つ与えよ.
⑵ $2$ 以上の自然数 $n,m$ が $n\lt m$ を満たすとき,
$$0\lt\dfrac{a_{n+1}}{a_n}-\dfrac{a_{m+1}}{a_m}\leqq 2C\left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right)$$となることを示せ.⑶ ある実数 $D$ が存在して,すべての自然数 $n$ について $a_{n+1}-a_n\leqq D$ となることを示せ.
⑷ ある自然数 $n_0$ が存在して,点 $\mathrm{A}_{n_0},\mathrm{A}_{n_0+1},\mathrm{A}_{n_0+2},\dots$ はすべて同一直線上にあることを示せ.
(京都大学)
※ 問題訂正を反映させたものを掲載しています。
解答
⑴
$a_n=n-1$ が条件を満たすことを示す。この数列はすべての自然数 $n$ について $0$ 以上の整数であり、$a_1=0, \ $$a_2=1$ を満たす。
まず、$\mathrm{A}_n(n-1,n), \ $$\mathrm{A}_{n+1}(n,n+1)$ であるから、直線 $\mathrm{OA}_n$ の傾きは $\dfrac{n}{n-1}=1+\dfrac{1}{n-1}$,直線 $\mathrm{OA}_{n+1}$ の傾きは $\dfrac{n+1}{n}=1+\dfrac{1}{n}$ となる。
$$1+\dfrac{1}{n-1}\gt1+\dfrac{1}{n}$$より、直線 $\mathrm{OA}_n$ と $\mathrm{OA}_{n+1}$ の傾きは一致しないので、$3$ 点 $\mathrm{A}_n,\mathrm{O},\mathrm{A}_{n+1}$ は同一直線上にない。また、$n$ が大きくなるにつれて直線 $\mathrm{OA}_n$ の傾きは狭義単調減少するので、三角形 $\mathrm{A}_n\mathrm{OA}_{n+1}$ と三角形 $\mathrm{A}_{n+1}\mathrm{OA}_{n+2}$ の内部が互いに交わることはない。よって、条件(ⅰ)を満たす。
次に
$$1+\dfrac{1}{n}\gt 1, \ \displaystyle\lim_{n\to\infty}\left(1+\dfrac{1}{n}\right)=1$$より、$\angle\mathrm{A}_1\mathrm{OA}_{n+1}\lt\dfrac{\pi}{4}$ かつ $\displaystyle\lim_{n\to\infty}\angle\mathrm{A}_1\mathrm{OA}_{n+1}=\dfrac{\pi}{4}$ であるから、条件(ⅲ)を満たす。
さらに、三角形 $\mathrm{A}_n\mathrm{OA}_{n+1}$ の面積は
$$\dfrac{1}{2}|n\cdot n-(n+1)(n-1)| = \dfrac{1}{2}\lt 100$$となる(補足1)ので、条件(ⅱ)を満たす。
以上より、条件を満たす数列 $\{a_n\}$ の例は $a_n=\boldsymbol{n-1}$ である。
$$\text{(例)}\boldsymbol{n-1}$$
⑵
条件(ⅰ)より、$n$ が大きくなるにつれて直線 $\mathrm{OA}_n$ の傾きは狭義単調減少するので、$n\lt m$ のとき、$\mathrm{A}_n(a_n,a_{n+1}), \ $$\mathrm{A}_m(a_m,a_{m+1})$ について
$$\begin{align}
\dfrac{a_{n+1}}{a_n} &\gt \dfrac{a_{m+1}}{a_m} \\
\therefore \ 0 &\lt \dfrac{a_{n+1}}{a_n}-\dfrac{a_{m+1}}{a_m} \quad\cdots\text{①}
\end{align}$$が成り立つ。
また、$k$ を $2$ 以上の自然数とすると、$\mathrm{A}_k(a_k,a_{k+1}), \ $$\mathrm{A}_{k+1}(a_{k+1},a_{k+2})$ であり、条件(ⅱ)より、三角形 $\mathrm{A}_k\mathrm{OA}_{k+1}$ の面積は $C$ より小さいので
$$\begin{align}
\dfrac{1}{2}|(a_{k+1})^2-a_ka_{k+2}| &\lt C \\
\therefore \ |(a_{k+1})^2-a_ka_{k+2}| &\lt 2C \quad\cdots\text{②}
\end{align}$$
ここで、条件(ⅰ),(ⅱ),(ⅲ)より、帰納的に点 $\mathrm{A}_2,\mathrm{A}_3,\mathrm{A}_4,\cdots$ はすべて
$$x\gt 0 \ \text{かつ} \ y\gt x$$の範囲に存在する。特に点 $\mathrm{A}_k(a_k,a_{k+1})$ について $a_{k+1}\gt a_k$ が成り立つので、数列 $\{a_n\}$ は狭義単調増加であり、$a_k\geqq a_2=1$ となる。
また、各項は整数なので、$a_{k+1}-a_k\geqq 1$ であり、$C\geqq 1$ に注意すると $2C\leqq 2C(a_{k+1}-a_k)$ が成り立つ。
よって、②より
$$|(a_{k+1})^2-a_ka_{k+2}| \leqq 2C(a_{k+1}-a_k)$$が成り立ち、この両辺を $a_ka_{k+1}$( $\gt 0$ )で除すと
$$\left| \dfrac{a_{k+1}}{a_k}-\dfrac{a_{k+2}}{a_{k+1}} \right|\leqq 2C\left(\dfrac{1}{a_k}-\dfrac{1}{a_{k+1}}\right)$$となる。①より $\dfrac{a_{k+1}}{a_k}-\dfrac{a_{k+2}}{a_{k+1}}\gt 0$ なので
$$\dfrac{a_{k+1}}{a_k}-\dfrac{a_{k+2}}{a_{k+1}} \leqq 2C\left(\dfrac{1}{a_k}-\dfrac{1}{a_{k+1}}\right)$$となる。この不等式に $k=n,n+1,\cdots,m-1$ をそれぞれ代入して、辺々足すと
$$\dfrac{a_{n+1}}{a_n}-\dfrac{a_{m+1}}{a_m}\leqq 2C\left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \quad\cdots\text{③}$$となる。
①,③より、与不等式が示された。$$\tag{証明終}$$
⑶
⑵の不等式より、$2\leqq n\lt m$ のとき
$$\begin{align}
\dfrac{a_{n+1}}{a_n}-\dfrac{a_{m+1}}{a_m} &\leqq 2C\left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \leqq \dfrac{2C}{a_n} \\
\dfrac{a_{n+1}}{a_n}-1 &\leqq \dfrac{a_{m+1}}{a_m}-1+\dfrac{2C}{a_n} \\
a_{n+1}-a_n &\leqq \left(\dfrac{a_{m+1}}{a_m}-1\right)a_n+2C \ \text{(}\because a_n\geqq 1 \ \text{)}
\end{align}$$が成り立つ。
ここで、条件(ⅲ)より
$$\displaystyle\lim_{m\to\infty}\dfrac{a_{m+1}}{a_m}=1$$であり、$m$ については $n$ より大きい自然数を任意に選べることに注意すると、十分大きい $m$ をとることで
$$\dfrac{a_{m+1}}{a_m}-1\leqq\dfrac{1}{a_n}$$を満たすことができる。
すなわち、$2$ 以上の自然数 $n$ について
$$a_{n+1}-a_n \leqq 2C+1$$となり、これは $n=1$ のときも成り立つ。
したがって、$D=2C+1$ とすれば、すべての自然数 $n$ について $a_{n+1}-a_n\leqq D$ となる。$$\tag{証明終}$$
⑷
数列 $\{a_n\}$ は整数からなる狭義単調増加な数列であり、⑶より $a_{n+1}-a_n\leqq D$ が成り立つので、直線 $\mathrm{A}_n\mathrm{A}_{n+1}$ の傾き $\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}$ がとりうる値は有限個である。この有限個の値のうち、$1$ より大きいものの最小値を $M$ とおく。
直線 $\mathrm{OA}_n$ の傾き $\dfrac{a_{n+1}}{a_n}$ は狭義単調減少であり
$$\displaystyle\lim_{n\to\infty}\dfrac{a_{n+1}}{a_n}=1$$なので、直線 $\mathrm{OA}_\ell$ の傾きについて $\dfrac{a_{\ell+1}}{a_\ell}\lt M$ を満たす実数 $\ell$( $\geqq 2$ )が存在する。このとき、$n\geqq \ell$ ならば $\dfrac{a_{n+1}}{a_n}\lt M$ となる。
$n\geqq\ell$ のとき、直線 $\mathrm{A}_n\mathrm{A}_{n+1}$ の傾き $\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}$ が $M$ 以上であると仮定すると、$\dfrac{a_{n+2}}{a_{n+1}}\geqq\dfrac{a_{n+1}}{a_n}$ となり、条件(ⅰ)に反する。
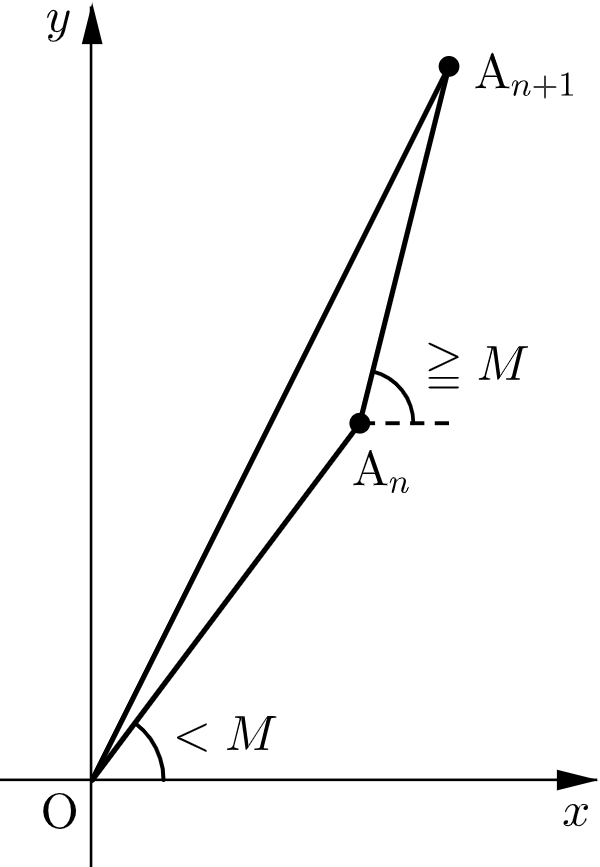
よって、$n\geqq\ell$ のとき
$$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}\leqq 1$$が成り立つ。
ここで、$n\geqq\ell$ において
$$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}\lt 1$$となるような $n$ が無限個存在すると仮定すると、そのような $n$ に対して
$$a_{n+1}-a_{n}\gt a_{n+2}-a_{n+1}$$が成り立つ。仮定より、この不等式は無限個成り立つが、それは $a_{n+1}-a_n$ が整数かつ $1$ 以上であることに矛盾する。(補足2)
したがって、$$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}\lt 1$$となるような $n$ は有限個であり、そのような $n$ の最大値を $N$ とすると、$n\geqq N+1$ において
$$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}=1$$である。
以上より、$n_0=N+1$ とすれば、点 $\mathrm{A}_{n_0},\mathrm{A}_{n_0+1},\mathrm{A}_{n_0+2},\cdots$ はすべて同一直線上にある。$$\tag{証明終}$$
解説
まず、条件(ⅰ)~(ⅲ)を的確に理解し、数式でどのように表されるかを考える必要があります。
⑴は、皆さんとりあえず $n-1$ を考えるのではないでしょうか?
具体例を通して問題設定を把握させる問題です。
⑵は、不等式の形から、部分分数分解の問題などで出てくる「 $-$ と $+$ が打ち消しあって結局最初と最後だけ残る」という形を想像できれば大丈夫です(今回は部分分数分解自体はしませんが)。
⑶は、解答のように直接 $D$ を構成してもいいですし、背理法によって矛盾が起こることを示してもいいです。条件(ⅲ)をどう使うかがポイントです。
⑷は、「数列 $\{a_n\}$ が整数からなる」ということが効いてきます。点 $\mathrm{A}_{n_0}$ 以降すべての点が同一直線上にあるということは、それ以降の $2$ 点間の傾きが一定ということですから、⑶の式を使えそうな感じがします。
文字が多く混乱しますが、$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}$ が $1$ 以上となる $n$ も、$1$ 未満となる $n$ も、有限個しかないことをうまく示しましょう。
補足
〔1〕
$3$ 点 $\mathrm{O}, \ $$\mathrm{P}(a,b), \ $$\mathrm{Q}(c,d)$ を頂点とする三角形 $\mathrm{OPQ}$ の面積 $S$ は
$$S=\dfrac{1}{2}|ad-bc|$$により求められます。
点の情報が座標で与えられているときに有効な面積計算の方法です。
(解答へ戻る)
〔2〕
$n\geqq\ell$ のとき
$$\dfrac{a_{n+2}-a_{n+1}}{a_{n+1}-a_{n}}\leqq 1$$すなわち「 $a_{n+1}-a_{n}=a_{n+2}-a_{n+1}$ 」または「 $a_{n+1}-a_{n}\gt a_{n+2}-a_{n+1}$ 」のどちらかが成り立ちます。後者が成り立つような $n$ を小さい方から $p_1,p_2,\cdots$ とすると、仮定より、$p_1,p_2,\cdots$ はすべて $\ell$ 以上かつ無限個あります。
ここで、$n=\ell$ のとき
$$a_{n+1}-a_{n}=L$$であるとします( $L$ は自然数)。
仮定より、$\ell\leqq n\leqq p_1-1$ の範囲では
$$\begin{align}
a_{\ell+1}-a_{\ell} &= a_{\ell+2}-a_{\ell-1} \\
&= \cdots \\
&= a_{p_1}-a_{p_1-1}\\
&= a_{p_1+1}-a_{p_1} = L
\end{align}$$が成り立ちますが、$n=p_1$ のとき
$$L = a_{p_1+1}-a_{p_1}\gt a_{p_1+2}-a_{p_1+1}$$となり、$a_{n+1}-a_{n}$ が整数であることから
$$L-1\geqq a_{p_1+2}-a_{p_1+1}$$となり、上限値が $1$ だけ減少します。
$n=p_2,p_3,\cdots$ のとき、同様に「上限値の減少」が起こるとすると、いずれ
$$0\geqq a_{n+1}-a_{n}$$となり、$a_{n+1}-a_{n}\geqq 1$ との矛盾が起こってしまいます。
(解答へ戻る)
まとめ
今回は、京都大学理学部特色入試・数学(2021年度 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
京都大学 理学部特色入試(数学)2021年度 第1問 解説
京都大学 理学部特色入試(数学)2021年度 第2問 解説
京都大学 理学部特色入試(数学)2021年度 第3問 解説
京都大学 理学部特色入試(数学)2021年度 第4問 解説













