東京大学理系数学 2022年第5問解説

ゆーきち

こんにちは、ゆーきちです！

今回は、東京大学理系数学（2022年第5問）の解説をしたいと思います。

Contents

問題
解答
解説
まとめ

問題

　座標空間内の点 $\mathrm{A}(0,0,2)$ と点 $\mathrm{B}(1,0,1)$ を結ぶ線分 $\mathrm{AB}$ を $z$ 軸のまわりに $1$ 回転させて得られる曲面を $S$ とする。$S$ 上の点 $\mathrm{P}$ と $xy$ 平面上の点 $\mathrm{Q}$ が $\mathrm{PQ}=2$ を満たしながら動くとき，線分 $\mathrm{PQ}$ の中点 $\mathrm{M}$ が通過しうる範囲を $K$ とする。 $K$ の体積を求めよ。
（東京大学）

解答

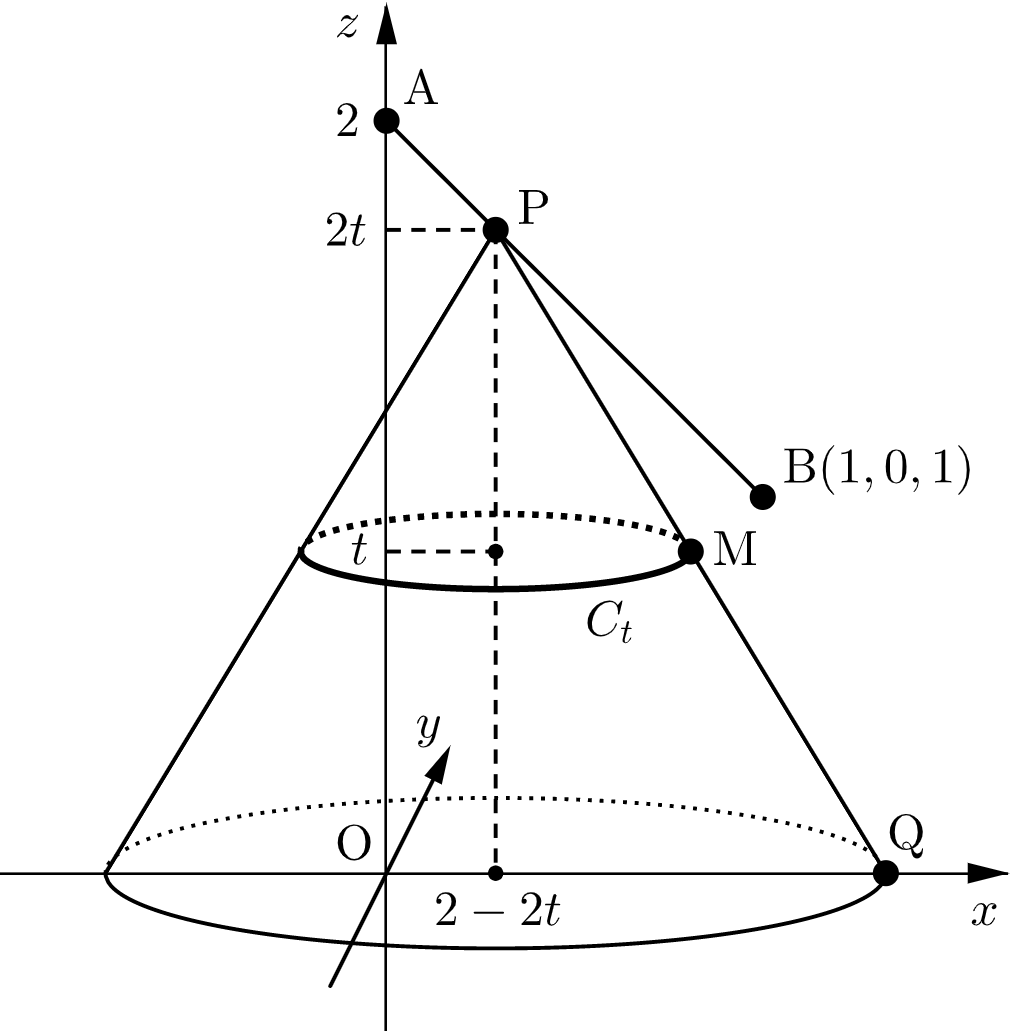
線分 $\mathrm{AB}$ の方程式は
$$z=2-x \text{（} \ 0\leqq x\leqq 1 \ \text{）},\quad y=0$$である。

$\mathrm{P}$ が線分 $\mathrm{AB}$ 上にある場合を考えると、実数 $t\left(\text{ただし} \ \dfrac{1}{2}\leqq t\leqq 1\right)$ を用いて、$\mathrm{P}$ の座標は $(2-2t,0,2t)$ と表せる。

$\mathrm{M}$ は線分 $\mathrm{PQ}$ の中点なので、$\mathrm{PM}=1$ である。

$\mathrm{Q}$ が $xy$ 平面上を動くとき、$\mathrm{M}$ は平面 $z=t$ 上を動き、その軌跡は $\mathrm{P}$ を中心とする半径 $1$ の球面と平面 $z=t$ の交円 $C_t$ となる。

$C_t$ の中心の座標は $(2-2t,0,t)$、半径は三平方の定理より $\sqrt{1-t^2}$ であり、これを $z$ 軸のまわりに $1$ 回転させた領域が、$K$ を平面 $z=t$ で切った断面となる。

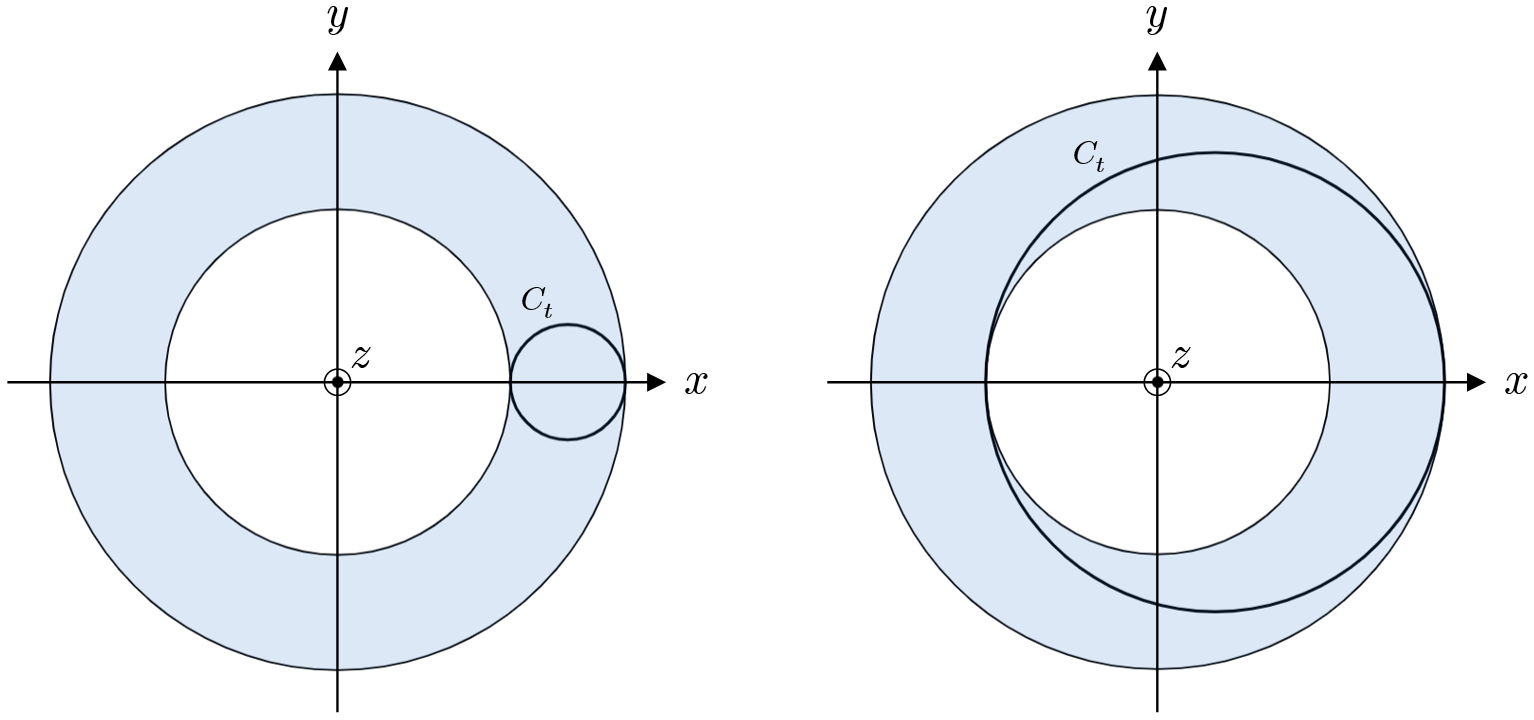
平面 $z=t$ 上で、$z$ 軸が $C_t$ の外部にある場合（上左図）と内部にある場合（上右図）があるが、いずれにせよ $C_t$ を $z$ 軸のまわりに $1$ 回転させると、半径 $(2-2t)+\sqrt{1-t^2}$ の円と半径 $\left|(2-2t)-\sqrt{1-t^2}\right|$ の円（ともに中心 $(0,0,t)$ ）で挟まれた領域となる。
この領域の面積を $S(t)$ とおくと
$$\begin{eqnarray}
S(t) &=& \pi\left\{(2-2t)+\sqrt{1-t^2}\right\}^2 – \ \pi\left\{(2-2t)-\sqrt{1-t^2}\right\}^2 \\
&=& 4\pi(2-2t)\sqrt{1-t^2}
\end{eqnarray}$$

よって、求める体積 $V$ は
$$\begin{eqnarray}
V &=& \displaystyle\int_\frac{1}{2}^1 S(t)dt \\
&=& \displaystyle\int_\frac{1}{2}^1 4\pi(2-2t)\sqrt{1-t^2}dt \\
&=& 8\pi\left(\displaystyle\int_\frac{1}{2}^1 \sqrt{1-t^2}dt -\displaystyle\int_\frac{1}{2}^1 t\sqrt{1-t^2}dt\right)
\end{eqnarray}$$

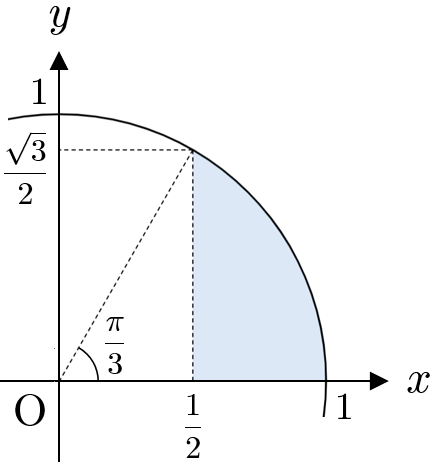
ここで、$\displaystyle\int_\frac{1}{2}^1 \sqrt{1-t^2}dt$ は右図の網掛け部分の面積に等しいので
$$\begin{eqnarray}
&& \displaystyle\int_\frac{1}{2}^1 \sqrt{1-t^2}dt \\
&=& \dfrac{1}{2}\cdot 1^2 \cdot \dfrac{\pi}{3} \ – \ \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{\sqrt{3}}{2} \\
&=& \dfrac{\pi}{6} \ – \ \dfrac{\sqrt{3}}{8}
\end{eqnarray}$$

また
$$\begin{eqnarray}
\displaystyle\int_\frac{1}{2}^1 t\sqrt{1-t^2}dt &=& \left[-\dfrac{1}{3}\left(1-t^2\right)^\frac{3}{2}\right]_\frac{1}{2}^1 \\
&=& \dfrac{1}{3}\cdot\left(\dfrac{3}{4}\right)^\frac{3}{2} \\
&=& \dfrac{\sqrt{3}}{8}
\end{eqnarray}$$

したがって
$$\begin{eqnarray}
V &=& 8\pi\bigg(\dfrac{\pi}{6} \ – \ \dfrac{\sqrt{3}}{8} \ – \ \dfrac{\sqrt{3}}{8}\bigg) \\
&=& \boldsymbol{\dfrac{4}{3}\pi^2-2\sqrt{3}\pi}
\end{eqnarray}$$

答え

$$\boldsymbol{\dfrac{4}{3}\pi^2-2\sqrt{3}\pi}$$

解説

図の情報を端的かつ的確に説明して、解答の方針を明確にしましょう。

動かす図形が多いので混乱しそうですが、固定したものを $1$ つ $1$ つ動かして、どのような図形が得られるかを追っていけば大丈夫です。

また、最終的な図形（今回でいえば $K$ ）が立体の場合、その全体像を把握する必要はないです。なぜなら重要なのはその「断面」であり、全体像を把握せずとも積分によって体積を求められるからです。その際の断面は、必ず回転軸に対して垂直に切りましょう。今回の問題では悩まずとも $z$ 軸に垂直に（平面 $z=t$ で）切るでしょうが、中には斜めの軸に回転させる問題もあります。その際も断面は必ず回転軸に対して垂直でなければならないので注意しましょう。

なお、$V$ を立式した後は、置換積分によっても値を求めることができ、以下に示します：

$$V=8\pi\displaystyle\int_\frac{1}{2}^1 (1-t)\sqrt{1-t^2}dt$$に対して、$t=\sin\theta$ とおくと
$$dt=\cos\theta \ d\theta \qquad
\begin{array}{c|c} \hline
t & \dfrac{1}{2} \to 1 \\
\hline
\theta & \dfrac{\pi}{6} \to \dfrac{\pi}{2} \\
\hline
\end{array}$$より
$$\begin{eqnarray}
V &=& 8\pi\displaystyle\int_\frac{1}{2}^1 (1-t)\sqrt{1-t^2}dt \\
&=& 8\pi\displaystyle\int_\frac{\pi}{6}^\frac{\pi}{2} (1-\sin\theta)\sqrt{1-\sin^2\theta}\cos\theta \ d\theta \\
&=& 8\pi\displaystyle\int_\frac{\pi}{6}^\frac{\pi}{2} (1-\sin\theta)\cos\theta\cdot\cos\theta \ d\theta \\
&=& 8\pi\displaystyle\int_\frac{\pi}{6}^\frac{\pi}{2} \left(\cos^2\theta-\sin\theta\cos^2\theta\right) d\theta \\
&=& 8\pi\displaystyle\int_\frac{\pi}{6}^\frac{\pi}{2} \left\{\dfrac{1+\cos 2\theta}{2}+(\cos\theta)’\cos^2\theta \right\} d\theta \\
&=& 8\pi\left[ \dfrac{1}{2}\theta + \dfrac{\sin 2\theta}{4} + \dfrac{\cos^3\theta}{3} \right]_\frac{\pi}{6}^\frac{\pi}{2} \\
&=& 8\pi\bigg\{ \dfrac{1}{2}\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)-\dfrac{1}{4}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{1}{3}\cdot\dfrac{3\sqrt{3}}{8} \bigg\} \\
&=& \dfrac{4}{3}\pi^2-2\sqrt{3}\pi
\end{eqnarray}$$