今回は、京都大学理学部特色入試・数学(2023年度 第3問)の解説をしたいと思います。
問題
複素数の数列 $\{z_n\}$ に対する次の $2$ つの条件を考える.
(ⅰ) すべての自然数 $n$ に対して,$|z_n-z_{n+1}|=2^n$ が成り立つ.
(ⅱ) すべての自然数 $n$ に対して,
$$\dfrac{(z_{n}-z_{n+1})(z_{n+2}-z_{n+3})}{(z_{n+1}-z_{n+2})(z_{n+3}-z_{n})}$$は実数である.複素数の数列 $\{z_n\}$ で(ⅰ)と(ⅱ)をともに満たすものをすべて考えたとき,
(京都大学)
$$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$$がとり得る値をすべて求めよ.
解答
複素数の数列 $\{z_n\}$ が(ⅰ),(ⅱ)をともに満たすとする。
(ⅰ)より、(ⅱ)の分子については
$$(z_{n}-z_{n+1})(z_{n+2}-z_{n+3})\ne0.$$
また、(ⅱ)より
$$\dfrac{(z_{n}-z_{n+1})(z_{n+2}-z_{n+3})}{(z_{n+1}-z_{n+2})(z_{n+3}-z_{n})}=\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}\cdot\dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}$$となり、これが実数なので
$$\arg\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}+\arg\dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}=0,\,\pi. \ \cdots\text{①}$$ただし、角度に関する等式については $2\pi$ の整数倍の差を無視するとする(以下同様)。
ここで、$\mathrm{A}(z_n), \ $$\mathrm{B}(z_{n+1}), \ $$\mathrm{C}(z_{n+2}), \ $$\mathrm{D}(z_{n+3})$ とおく。
⑴ $\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}$ が実数であるとき$$\arg\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}=0,\,\pi$$より、複素数平面上において $3$ 点 $\mathrm{B},\,$$\mathrm{C},\,$$\mathrm{D}$ は同一直線上にある。
また、①より
$$\arg\dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}=0,\,\pi$$となるので、同様に、$3$ 点 $\mathrm{D},\,$$\mathrm{A},\,$$\mathrm{B}$ は同一直線上にある。
よって、$4$ 点 $\mathrm{A},\,$$\mathrm{B},\,$$\mathrm{C},\,$$\mathrm{D}$ は同一直線上の点となる。
⑵ $\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}$ が実数でないとき
$$\arg\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}\ne0,\,\pi$$より、複素数平面上において $3$ 点 $\mathrm{B},\,$$\mathrm{C},\,$$\mathrm{D}$ は同一直線上にない。
また、①より
$$\arg\dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}\ne0,\,\pi$$となるので、同様に、$3$ 点 $\mathrm{D},\,$$\mathrm{A},\,$$\mathrm{B}$ は同一直線上にない。
さらに、①より
$$\begin{array}{l}
\text{㋐} \ \angle\mathrm{BCD}=\angle\mathrm{BAD} \\
\text{㋑} \ \angle\mathrm{BCD}+\angle\mathrm{DAB}=\pi
\end{array}$$のいずれかが成り立つ。ただし、角度は反時計回りを正とする。
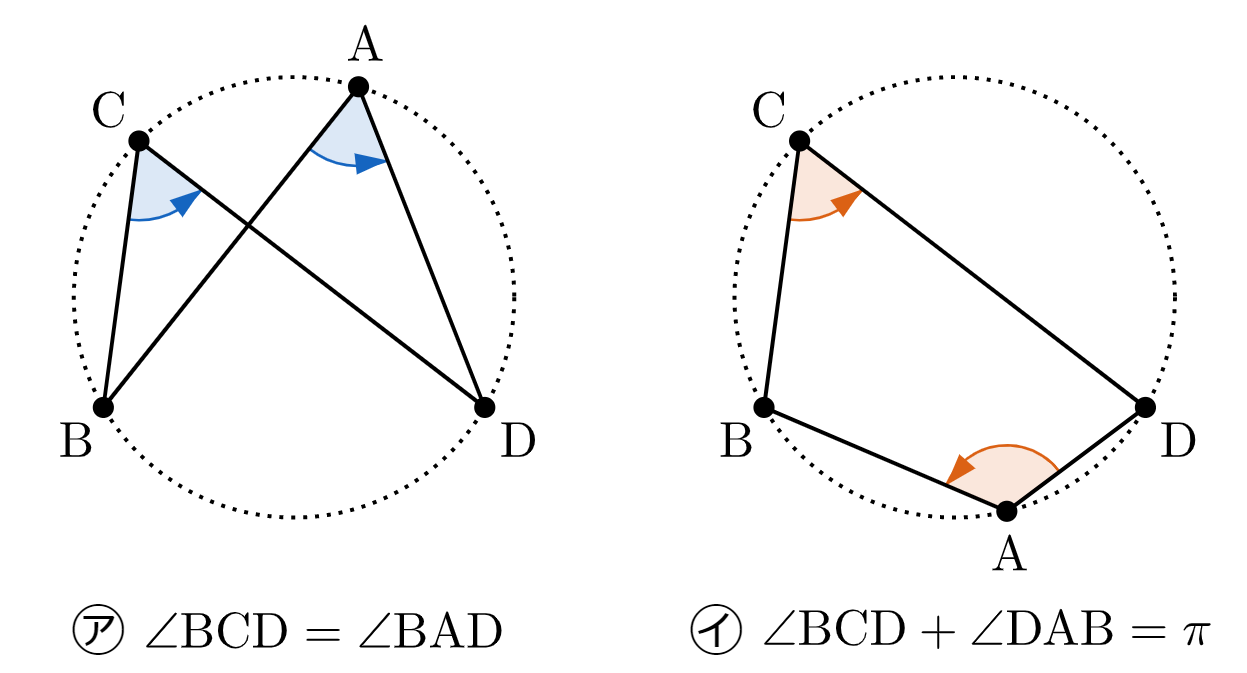
上図より、いずれの場合も $4$ 点 $\mathrm{A},\,$$\mathrm{B},\,$$\mathrm{C},\,$$\mathrm{D}$ は同一円周上の点となる。
⑴,⑵より、改めて $\mathrm{A}_n(z_n)$ とおくと、すべての自然数 $n$ に対して $4$ 点 $\mathrm{A}_n,\,$$\mathrm{A}_{n+1},\,$$\mathrm{A}_{n+2},\,$$\mathrm{A}_{n+3}$ は同一直線上もしくは同一円周上に位置する。
ここで、$4$ 点 $\mathrm{A}_1,\,$$\mathrm{A}_2,\,$$\mathrm{A}_3,\,$$\mathrm{A}_4$ が同一の円 $C$ の円周上にあると仮定する。
このとき、(ⅰ)より $3$ 点 $\mathrm{A}_2,\,$$\mathrm{A}_3,\,$$\mathrm{A}_4$ は相異なる点であり、同一直線上に位置することはないので、$\mathrm{A}_5$ を加えた $4$ 点 $\mathrm{A}_2,\,$$\mathrm{A}_3,\,$$\mathrm{A}_4,\,$$\mathrm{A}_5$ は同一円周上に位置することが分かる。
この円は $\triangle\mathrm{A}_2\mathrm{A}_3\mathrm{A}_4$ の外接円、すなわち $C$ であるから、$\mathrm{A}_5$ も $C$ 上の点となる。
したがって、帰納的にすべての点 $\mathrm{A}_n$ は $C$ 上に位置し、$2$ 点 $\mathrm{A}_n,\,$$\mathrm{A}_{n+1}$ 間の距離が $C$ の直径を超えることはない。
しかし、(ⅰ)より
$$\displaystyle\lim_{n\to\infty}|z_n-z_{n+1}|=\infty$$であるから、矛盾する。
よって、$4$ 点 $\mathrm{A}_1,\,$$\mathrm{A}_2,\,$$\mathrm{A}_3,\,$$\mathrm{A}_4$ は同一直線上に位置し、帰納的にすべての点 $\mathrm{A}_n$ は同一直線上に位置すると分かる。
以上より
$$\arg\dfrac{z_{2022}-z_{2023}}{z_{2024}-z_{2023}}=0,\,\pi$$となり $\dfrac{z_{2022}-z_{2023}}{z_{2024}-z_{2023}}$ は実数となるから、$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ も実数となる。$\cdots\text{②}$
さらに、(ⅰ)より
$$\begin{align}
\left|\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}\right| &= \dfrac{|z_{2022}-z_{2023}|}{|z_{2023}-z_{2024}|} \\[0.3em]
&= \dfrac{2^{2022}}{2^{2023}} = \dfrac{1}{2}
\end{align}$$であり、②より $\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ がとり得る値の候補は $\pm\dfrac{1}{2}$ となる。
ここで、$z_n=2^n$ とすると
$$\begin{align}
|z_n-z_{n+1}| &= |2^n-2^{n+1}| \\[0.2em]
&= |2^n\cdot(1-2)| \\[0.2em]
&= 2^n
\end{align}$$より、(ⅰ)を満たす。また、明らかに(ⅱ)を満たす。
このとき
$$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}} = \dfrac{2^{2022}-2^{2023}}{2^{2023}-2^{2024}} = \dfrac{1}{2}.$$
また、$z_n=\dfrac{(-2)^n}{3}$ とすると
$$\begin{align}
|z_n-z_{n+1}| &= \left|\dfrac{(-2)^n}{3}-\dfrac{(-2)^{n+1}}{3}\right| \\[0.2em]
&= \dfrac{|(-2)^n\cdot\{1-(-2)\}|}{3} \\[0.2em]
&= 2^n
\end{align}$$より、(ⅰ)を満たす。また、明らかに(ⅱ)を満たす。
このとき
$$\begin{align}
\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}} &= \dfrac{3z_{2022}-3z_{2023}}{3z_{2023}-3z_{2024}} \\[0.2em]
&= \dfrac{(-2)^{2022}-(-2)^{2023}}{(-2)^{2023}-(-2)^{2024}} \\[0.2em]
&= -\dfrac{1}{2}.
\end{align}$$
以上より、$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ がとり得る値は $\boldsymbol{\pm\dfrac{1}{2}}$ である。
$$\boldsymbol{\pm\dfrac{1}{2}}$$
解説
この問題は式変形を用いて計算で解くよりも、解答のように複素数平面上の図形に置き換えて解く方が解きやすいと思います。
条件(ⅰ)からは、隣り合う番号の点の間の距離がだんだん大きくなることが分かります。
条件(ⅱ)では、$\dfrac{\text{差}}{\text{差}}$ が出てきているので、偏角についての情報があると推測できます。
複素数平面上のすべての点 $\mathrm{A}_n$ が同一直線上に位置し、そこから $\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ は実数となることを示す議論はなかなか難しく、偏角についての式が表す意味や、確定した情報から帰納的に何が言えるかということについて思考が必要な問題です。
最後のところで、とり得る値の候補が $\pm\dfrac{1}{2}$ と分かったら、それを満たす $\{z_n\}$ が本当に存在するかの検証が必要です。
まとめ
今回は、京都大学理学部特色入試・数学(2023年度 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
京都大学 理学部特色入試(数学)2023年度 第1問 解説
京都大学 理学部特色入試(数学)2023年度 第2問 解説
京都大学 理学部特色入試(数学)2023年度 第3問 解説
京都大学 理学部特色入試(数学)2023年度 第4問 解説













