東京大学 理系数学 2023年 第3問 解説

今回は、東京大学理系数学（2023年 第3問）の解説をしたいと思います。

問題

　$a$ を実数とし，座標平面上の点 $(0,a)$ を中心とする半径 $1$ の円の周を $C$ とする。

⑴　$C$ が，不等式 $y\gt x^2$ の表す領域に含まれるような $a$ の範囲を求めよ。

⑵　$a$ は⑴で求めた範囲にあるとする。$C$ のうち $x\geqq0$ かつ $y\lt a$ を満たす部分を $S$ とする。$S$ 上の点 $\mathrm{P}$ に対し，点 $\mathrm{P}$ での $C$ の接線が放物線 $y=x^2$ によって切り取られてできる線分の長さを $L_{\mathrm{P}}$ とする。$L_{\mathrm{Q}}=L_{\mathrm{R}}$ となる $S$ 上の相異なる $2$ 点 $\mathrm{Q}, \ $$\mathrm{R}$ が存在するような $a$ の範囲を求めよ。

（東京大学）

解答

⑴

$C$ が，不等式 $y\gt x^2$ の表す領域に含まれるような $a$ の範囲を求めよ。

$C$ 上の任意の点 $(x,y)$ は
$$\left\{
\begin{eqnarray}
x &=& \cos\theta \\
y &=& \sin\theta+a
\end{eqnarray}
\right.\quad(0\leqq\theta\lt2\pi)$$と表される。

$C$ が $y\gt x^2$ の表す領域に含まれるための必要十分条件は、$0\leqq\theta\lt2\pi$ を満たすすべての $\theta$ に対し
$$\sin\theta+a\gt\cos^2\theta\quad\cdots\text{①}$$が成り立つことである。

①より
$$\begin{eqnarray}
a &\gt& -\sin\theta+(1-\sin^2\theta) \\
\therefore \ a &\gt& -\left(\sin\theta+\dfrac{1}{2}\right)^2+\dfrac{5}{4}.\quad\cdots\text{②}
\end{eqnarray}$$

$0\leqq\theta\lt2\pi$ において $-1\leqq\sin\theta\leqq1$ より、②の右辺は $\sin\theta=-\dfrac{1}{2}$ のとき最大値 $\dfrac{5}{4}$ をとる。

よって、求める $a$ の範囲は
$$\boldsymbol{a\gt\dfrac{5}{4}}.$$

⑵

$a$ は⑴で求めた範囲にあるとする。$C$ のうち $x\geqq0$ かつ $y\lt a$ を満たす部分を $S$ とする。$S$ 上の点 $\mathrm{P}$ に対し，点 $\mathrm{P}$ での $C$ の接線が放物線 $y=x^2$ によって切り取られてできる線分の長さを $L_{\mathrm{P}}$ とする。$L_{\mathrm{Q}}=L_{\mathrm{R}}$ となる $S$ 上の相異なる $2$ 点 $\mathrm{Q}, \ $$\mathrm{R}$ が存在するような $a$ の範囲を求めよ。

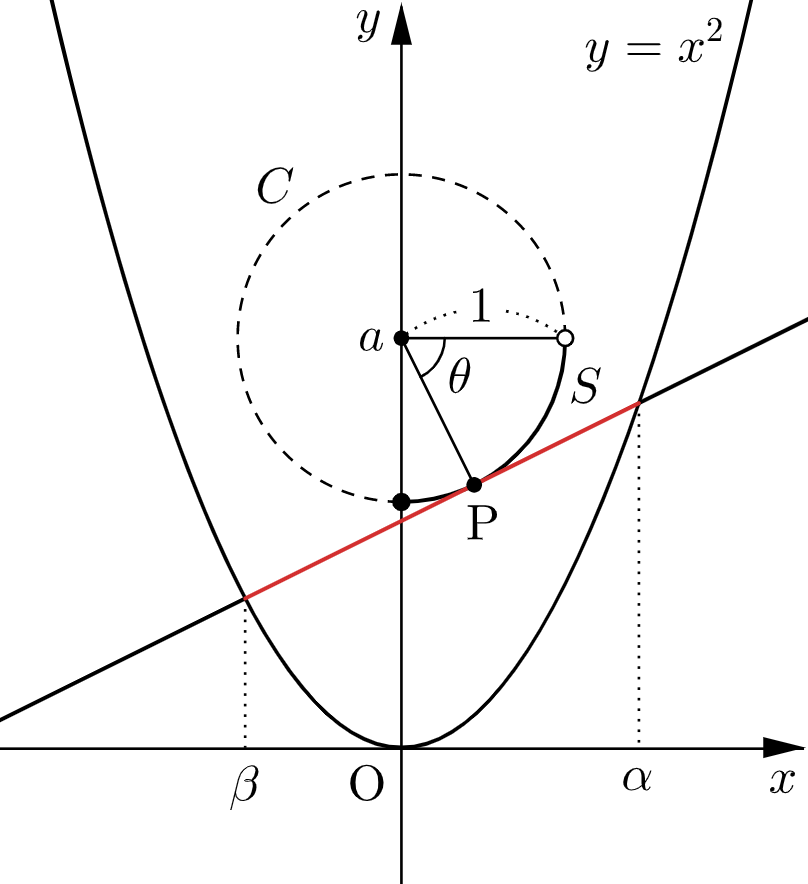
$S$ 上の任意の点 $\mathrm{P}(x,y)$ は
$$\left\{
\begin{eqnarray}
x &=& \cos\theta \\
y &=& \sin\theta+a
\end{eqnarray}
\right.\quad\left(-\dfrac{\pi}{2}\leqq\theta\lt0\right)$$と表される。

$C$ の方程式は
$$x^2+(y-a)^2=1$$であるから、点 $\mathrm{P}$ での $C$ の接線（$\,\ell$ とする）の方程式は
$$\begin{eqnarray}
(\cos\theta)x+\{(\sin\theta+a)-a\}(y-a) &=& 1 \\[0.3em]
\therefore \ (\cos\theta)x+(\sin\theta)y-a\sin\theta-1 &=& 0.
\end{eqnarray}$$

$\ell$ の方程式と $y=x^2$ から $y$ を消去すると
$$(\sin\theta)x^2+(\cos\theta)x-a\sin\theta-1=0.\quad\cdots\text{③}$$

放物線 $y=x^2$ のグラフが下に凸であり、$a\gt\dfrac{5}{4}$ において、$\ell$ が $y\gt x^2$ の表す領域にある点 $\mathrm{P}$ を通ることに注意すると、③は異なる $2$ つの実数解を持つ。その $2$ 解を $\alpha, \ $$\beta$（$\,\alpha\gt\beta\,$）とおくと、解と係数の関係により
$$\alpha+\beta=-\dfrac{\cos\theta}{\sin\theta}\,,\quad\alpha\beta=-a-\dfrac{1}{\sin\theta}$$が成り立つ。

$2$ 点 $(\alpha,\alpha^2)$，$(\beta,\beta^2)$ 間の距離が $L_{\mathrm{P}}$ であるから
$$\begin{eqnarray}
{L_{\mathrm{P}}}^2 &=& (\alpha-\beta)^2+(\alpha^2-\beta^2)^2 \\[0.2em]
&=& (\alpha-\beta)^2+(\alpha+\beta)^2(\alpha-\beta)^2 \\[0.2em]
&=& (\alpha-\beta)^2\{(\alpha+\beta)^2+1\} \\[0.2em]
&=& \{(\alpha+\beta)^2-4\alpha\beta\}\{(\alpha+\beta)^2+1\} \\[0.2em]
&=& \left\{\dfrac{\cos^2\theta}{\sin^2\theta}-4\left(-a-\dfrac{1}{\sin\theta}\right)\right\}\left(\dfrac{\cos^2\theta}{\sin^2\theta}+1\right) \\[0.2em]
&=& \left(\dfrac{1-\sin^2\theta}{\sin^2\theta}+4a+\dfrac{4}{\sin\theta}\right)\cdot\dfrac{1}{\sin^2\theta} \\[0.2em]
&=& \dfrac{1}{\sin^4\theta}+\dfrac{4}{\sin^3\theta}+\dfrac{4a-1}{\sin^2\theta}.
\end{eqnarray}$$

$t=\dfrac{1}{\sin\theta}$ とおくと、$-\dfrac{\pi}{2}\leqq\theta\lt0$ において $t\leqq-1$ であり、$\theta$ と $t$ は $1$ 対 $1$ 対応する。

このとき
$${L_{\mathrm{P}}}^2=t^4+4t^3+(4a-1)t^2$$であり、この式の右辺を $f(t)$ とおく。

$L_{\mathrm{P}}\gt0$ より、題意を満たす $2$ 点 $\mathrm{Q}, \ $$\mathrm{R}$ が存在するための必要十分条件は、$f(t)$ が異なる $t$ で同じ値を $2$ 回以上とること、すなわち $t\lt-1$ において $f(t)$ が極値をもつことである。

$$\begin{eqnarray}
f'(t) &=& 4t^3+12t^2+2(4a-1)t \\[0.2em]
&=& 2t(2t^2+6t+4a-1) \\[0.2em]
&=& 2t\left\{2\left(t+\dfrac{3}{2}\right)^2+4a-\dfrac{11}{2}\right\}.
\end{eqnarray}$$

(ⅰ)　$4a-\dfrac{11}{2}\lt0$ すなわち $\left(\dfrac{5}{4}\lt\right)\,a\lt\dfrac{11}{8}$ のとき

$t\lt-\dfrac{3}{2}$ の範囲で $f'(t)=0$ となる $t$ が存在し、その前後で $f'(t)$ の符号が変化するため、$t\lt-1$ の範囲で $f(t)$ は極値をとる。

(ⅱ)　$4a-\dfrac{11}{2}\geqq0$ すなわち $a\geqq\dfrac{11}{8}$ のとき

$t\lt-1$ において $f'(t)\lt0$ より、$f(t)$ は単調減少するため、$t\lt-1$ の範囲で $f(t)$ は極値をとらない。

(ⅰ),(ⅱ)より、求める $a$ の範囲は
$$\boldsymbol{\dfrac{5}{4}\lt a\lt\dfrac{11}{8}}.$$

解説

円と放物線というよくあるテーマの問題ですが、放物線によって切り取られた線分の長さが関わるところは目新しいです。

線分の長さを関数で表す際、扱いやすいように変数変換しておくと計算ミスを減らすことができます。

その後は、$L_{\mathrm{Q}}=L_{\mathrm{R}}$ となる $2$ 点 $\mathrm{Q}$，$\mathrm{R}$ が存在することをどう言い換えるかがポイントです。横軸を $t$ ，縦軸を $f(t)$ としたグラフなどをかいてみると、$f(t)$ が減少→増加（あるいは増加→減少）に転じる、つまり極値をもつことが必要十分条件だと分かると思います。

まとめ

今回は、東京大学理系数学（2023年 第3問）の解説をしました。