京都大学 理学部特色入試（数学）2023年度 第1問 解説

今回は、京都大学理学部特色入試・数学（2023年度 第1問）の解説をしたいと思います。

問題

　平面内の鋭角三角形 $\mathrm{△}\mathrm{ABC}$ を考える．$\mathrm{△}\mathrm{ABC}$ の内部の点 $\mathrm{P}$ に対して，

　　直線 $\mathrm{BC}$ に関して点 $\mathrm{P}$ と対称な点を $\mathrm{D}$，
　　直線 $\mathrm{CA}$ に関して点 $\mathrm{P}$ と対称な点を $\mathrm{E}$，
　　直線 $\mathrm{AB}$ に関して点 $\mathrm{P}$ と対称な点を $\mathrm{F}$

とする．$6$ 点 $\mathrm{A},$$\mathrm{B},$$\mathrm{C},$$\mathrm{D},$$\mathrm{E},$$\mathrm{F}$ が同一円周上にあるような $\mathrm{P}$ は $\mathrm{△}\mathrm{ABC}$ の内部にいくつあるか求めよ．

（京都大学）

解答

$\mathrm{△}\mathrm{ABC}$ の外心を $\mathrm{O}$ とし、外接円 $\mathrm{O}$ の半径を $R$ とする。

直線 $\mathrm{BC},$$\mathrm{CA},$$\mathrm{AB}$ に関して円 $\mathrm{O}$ と対称な円の中心をそれぞれ ${\mathrm{O}}_1,$${\mathrm{O}}_2,$${\mathrm{O}}_3$ とする。

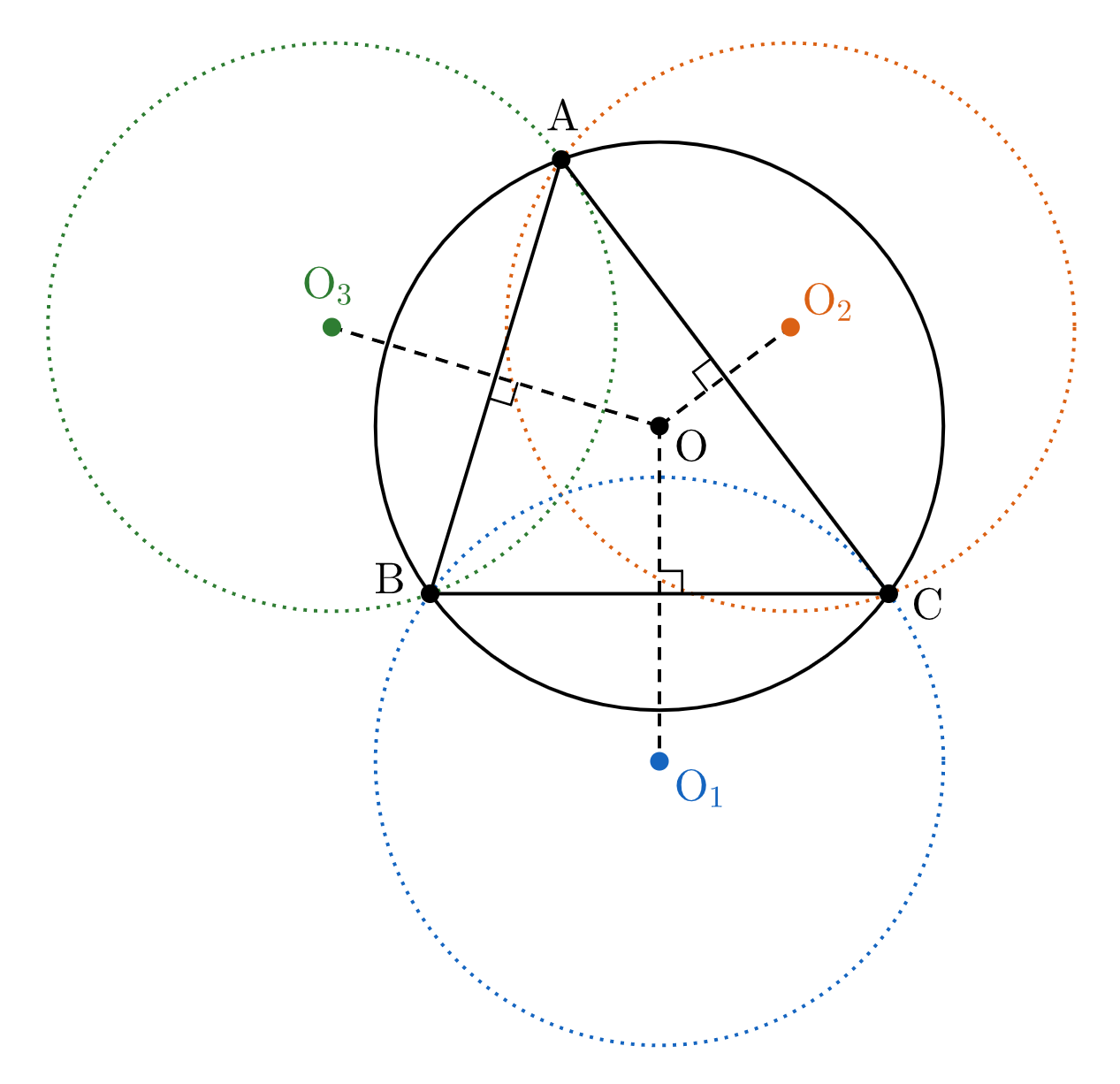
$\mathrm{△}\mathrm{ABC}$ の外接円は $1$ つなので、$6$ 点 $\mathrm{A},$$\mathrm{B},$$\mathrm{C},$$\mathrm{D},$$\mathrm{E},$$\mathrm{F}$ が同一円周上にあるとき、その円は円 $\mathrm{O}$ である。

ここで、点 $\mathrm{D}$ が円 $\mathrm{O}$ 上にあることと点 $\mathrm{P}$ が円 ${\mathrm{O}}_1$ 上にあることは同値である。

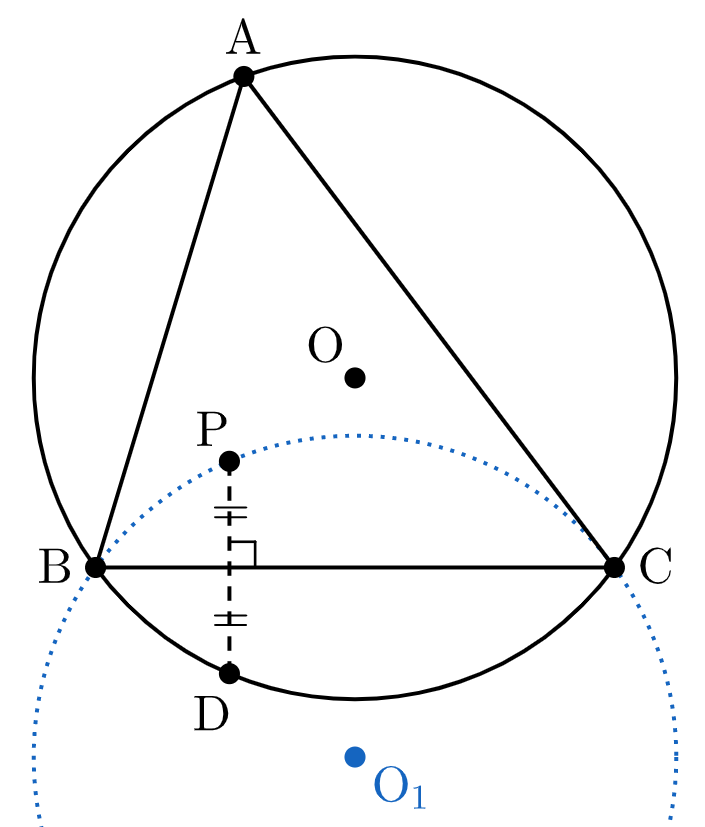
同様に考えると、点 $\mathrm{P}$ が条件を満たすのは、点 $\mathrm{P}$ が「円 ${\mathrm{O}}_1,$${\mathrm{O}}_2,$${\mathrm{O}}_3$ すべての円周上にある」$\cdots (\ast )$ ときである。

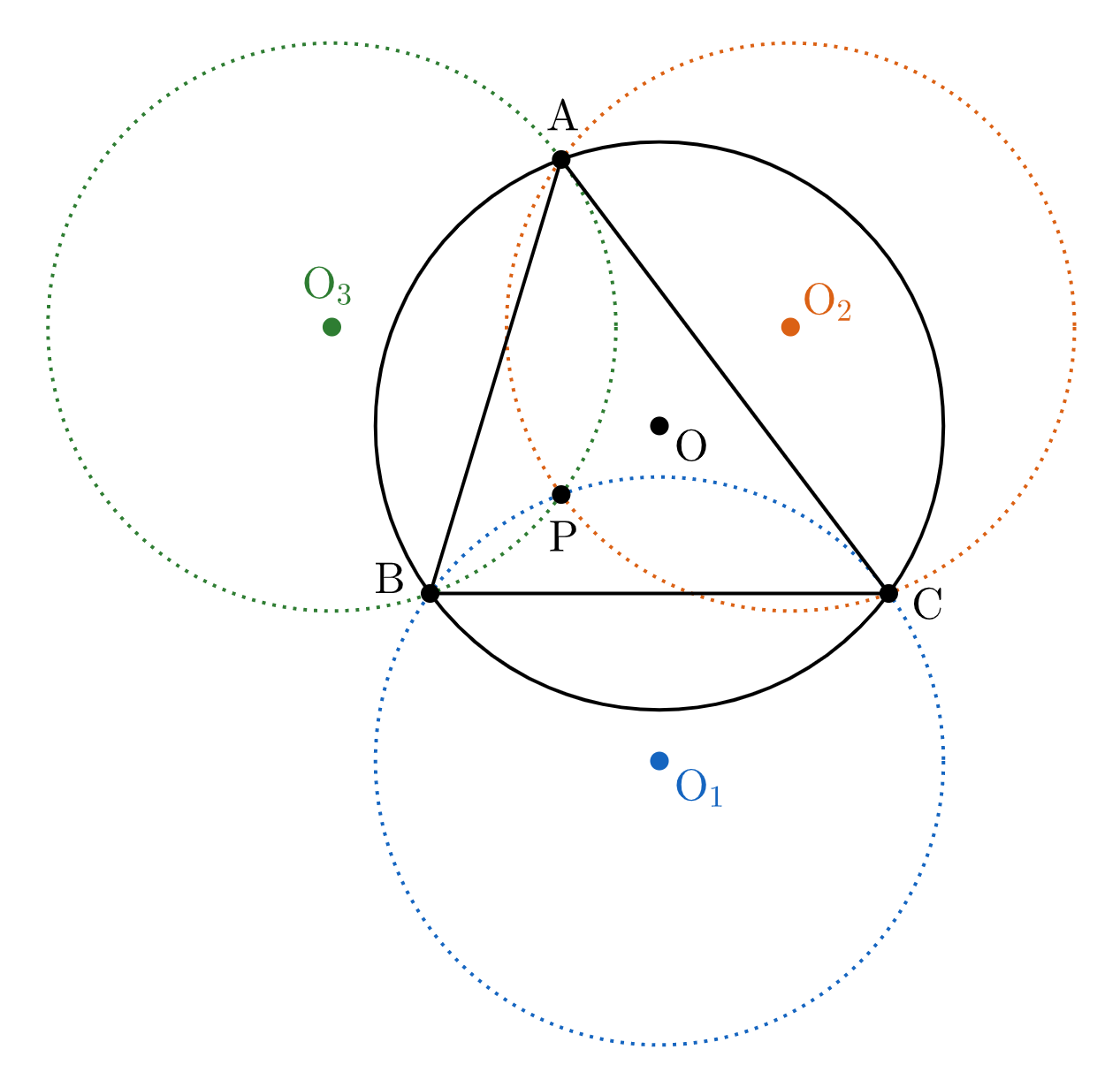
円 ${\mathrm{O}}_1,$${\mathrm{O}}_2,$${\mathrm{O}}_3$ の半径はすべて $R$ であり、これらの中心 ${\mathrm{O}}_1,$${\mathrm{O}}_2,$${\mathrm{O}}_3$ は互いに異なる点なので、$(\ast )$ を満たす点は $\mathrm{△}{\mathrm{O}}_1{\mathrm{O}}_2{\mathrm{O}}_3$ の外心に限られる。

よって、条件を満たす点 $\mathrm{P}$ の個数は高々 $1$ 個である。（補足1）

以下、点 $\mathrm{P}$ が $\mathrm{△}\mathrm{ABC}$ の垂心 $\mathrm{H}$ に一致するとき、題意を満たすことを示す。

下図のように、直線 $\mathrm{AH}$ と直線 $\mathrm{BC}$，円 $\mathrm{O}$ の交点（$\mathrm{A}$ と異なる）をそれぞれ $\mathrm{K},$$\mathrm{L}$，直線 $\mathrm{BH}$ と直線 $\mathrm{CA}$，円 $\mathrm{O}$ の交点（$\mathrm{B}$ と異なる）をそれぞれ $\mathrm{M},$$\mathrm{N}$ とする。

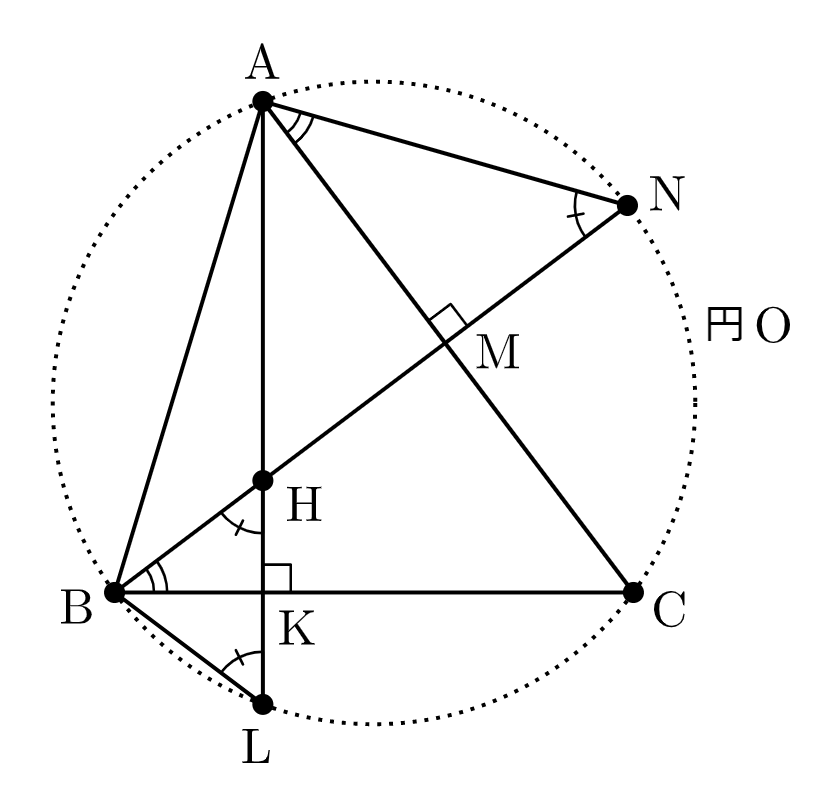
弧 $\mathrm{AB}$ に対する円周角の定理より
$$\mathrm{\angle }\mathrm{ALB}=\mathrm{\angle }\mathrm{ANB}.\cdots \text{①}$$弧 $\mathrm{CN}$ に対する円周角の定理より
$$\mathrm{\angle }\mathrm{CAN}=\mathrm{\angle }\mathrm{CBN}.\cdots \text{②}$$$\mathrm{H}$ は $\mathrm{△}\mathrm{ABC}$ の垂心なので$$\mathrm{\angle }\mathrm{AMN}=\mathrm{\angle }\mathrm{BKH}(={90}^{\circ }).\cdots \text{③}$$

①,②,③より
$$\begin{array}{rl}\mathrm{\angle }\mathrm{ALB}& =\mathrm{\angle }\mathrm{ANB}\\ & ={180}^{\circ }-\mathrm{\angle }\mathrm{CAN}-\mathrm{\angle }\mathrm{AMN}\\ & ={180}^{\circ }-\mathrm{\angle }\mathrm{CBN}-\mathrm{\angle }\mathrm{BKH}\text{（}\because \text{②,③）}\\ & =\mathrm{\angle }\mathrm{BHK}\end{array}$$となるので $\mathrm{△}\mathrm{BHL}$ は二等辺三角形であり、$\mathrm{BK}\perp \mathrm{HL}$ なので $\mathrm{HK}=\mathrm{KL}$ となる。

よって、直線 $\mathrm{BC}$ に関して点 $\mathrm{H}$ と対称な点は $\mathrm{L}$ に一致し、円 $\mathrm{O}$ 上に存在する。

同様に考えると、直線 $\mathrm{BC},$$\mathrm{CA},$$\mathrm{AB}$ に関して点 $\mathrm{H}$ と対称な点はすべて円 $\mathrm{O}$ 上に存在する。

以上より、点 $\mathrm{P}$ が $\mathrm{△}\mathrm{ABC}$ の垂心 $\mathrm{H}$ に一致するとき、題意を満たすことが示された。

また、$\mathrm{△}\mathrm{ABC}$ は鋭角三角形なので、その垂心は $\mathrm{△}\mathrm{ABC}$ の内部にある。

よって、求める点 $\mathrm{P}$ の個数は $\mathbf{1}\mathbf{\text{個}}$である。

解説

幾何や必要十分条件についての発想・理解が必要となる問題です。

問題設定は分かりやすいですが、解法の糸口がやや見えづらいかもしれません。点 $\mathrm{P}$ によって $\mathrm{D},$$\mathrm{E},$$\mathrm{F}$ がどこに移るかではなく、逆に、$\mathrm{D},$$\mathrm{E},$$\mathrm{F}$ が同一円周上の点であるときに点 $\mathrm{P}$ が満たすべき存在範囲はどこか、という視点で絞り込むのがポイントです。

条件を満たす点 $\mathrm{P}$ が高々 $1$ 個（存在しないか、存在したとしても $1$ 個）だと分かれば、あとは点 $\mathrm{P}$ が実際に存在することの証明です。

私がこれを解いたとき、点 $\mathrm{P}$ は $\mathrm{△}\mathrm{ABC}$ の垂心に一致すれば条件を満たすのでは？と思ったことがきっかけで解けたので、本解答でも垂心が題意を満たすことの証明を（突拍子もなく）しています。

補足

〔1〕
この時点では $\mathrm{△}{\mathrm{O}}_1{\mathrm{O}}_2{\mathrm{O}}_3$ の外心が $\mathrm{△}\mathrm{ABC}$ の内部にあるかどうかは分からないので「高々 $1$ 個」とまでしか言えません。
（解答へ戻る）

まとめ

今回は、京都大学理学部特色入試・数学（2023年度 第1問）の解説をしました。