【高校生クイズ計算問題に挑戦⑧】宇宙エレベーターの移動時間

今回は、高校生クイズで出題された計算問題にチャレンジしてみます。

問題

宇宙エレベーターで静止衛星までの移動にかかる時間を計算しなさい。
ただし、条件は以下のとおりとする。

ヒント

1. 等加速度直線運動の公式を使いましょう。
   初速 $v_0$ で移動を開始した物体が、一定の加速度 $a$ で時間 $t$ ・距離 $x$だけ直線運動した結果、速度が $v$ になったとすると、以下の式が成り立ちます。
   ・$v = v_0 + at$
   ・$x = v_0t + \dfrac{1}{2}at^2$
2. $v-t$ 図を使う方法もあります。
   $v-t$ 図においてグラフで囲まれた面積は、移動距離を表します。

解答

解法1

等加速度直線運動の公式を用いる方法です。

エレベーターが静止した状態（初速 $0$ ）から $0.1 \ [\mathrm{G}]$ で $100$ 秒間（$=t_1$ とする）加速した後の最高速度を $v \ [\mathrm{m/s}]$ とすると
$$\begin{eqnarray}
v &=& \underbrace{ 0 }_{ v_0 } + \underbrace{ (0.1 \times 9.8) \times 100 }_{ at } \\[0.5em]
&=& 98 \ [\mathrm{m/s}]
\end{eqnarray}$$

また、加速中にエレベーターが移動する距離を $d_1 \ [\mathrm{m}]$ とすると
$$\begin{eqnarray}
d_1 &=& \underbrace{ 0 \times 100 }_{ v_0t } + \underbrace{ \dfrac{1}{2} \times (0.1 \times 9.8) \times 100^2 }_{ \frac{1}{2}at^2 } \\
&=& 4900 \ [\mathrm{m}]
\end{eqnarray}$$

次に、エレベーターが減速している時間を $t_3 \ [\mathrm{s}]$ とすると
$$\begin{eqnarray}
0 &=& \underbrace{ 98 }_{ v_0 } + \underbrace{ (-0.01 \times 9.8) t_3 }_{ at } \\[0.5em]
t_3 &=& 1000 \ [\mathrm{s}]
\end{eqnarray}$$

また、減速中にエレベーターが移動する距離を $d_3 \ [\mathrm{m}]$ とすると
$$\begin{eqnarray}
d_3 &=& \underbrace{ 98 \times 1000 }_{ v_0t } + \underbrace{ \dfrac{1}{2} \times (-0.01 \times 9.8) \times 1000^2 }_{ \frac{1}{2}at^2 } \\
&=& 49000 \ [\mathrm{m}]
\end{eqnarray}$$

よって、エレベーターが等速移動する距離を $d_2 \ [\mathrm{m}]$ とすると$$\begin{eqnarray}
d_1 + d_2 + d_3 &=& 36000 \times 10^3 \\[0.5em]
d_2 &=& 36000000 \ – \ (d_1 + d_3) \\
&=& 36000000 \ – \ (4900 + 49000) \\
&=& 35946100 \ [\mathrm{m}]
\end{eqnarray}$$

したがって、エレベーターが等速移動している時間を $t_2 \ [\mathrm{s}]$ とすると
$$\begin{eqnarray}
t_2 &=& \dfrac{d_2}{v} = \dfrac{35946100}{98} \\
&=& 366796.9 \\
&=& 366797 \ [\mathrm{s}]
\end{eqnarray}$$

以上より、エレベーターが静止衛星まで移動するのにかかる時間は
$$\begin{eqnarray}
t_1 + t_2 + t_3 &=& 100 + 366797 + 1000 \\
&=& 367897 \ [\mathrm{s}] \\
&=& \mathbf{102 \ [h] \ 11 \ [m] \ 37 \ [s]}
\end{eqnarray}$$

解法2

$\boldsymbol{ v-t }$ 図を用いる方法です。

縦軸を$v$（速度）、横軸を $t$（時間）とすると、グラフの概形は下図のようになります。

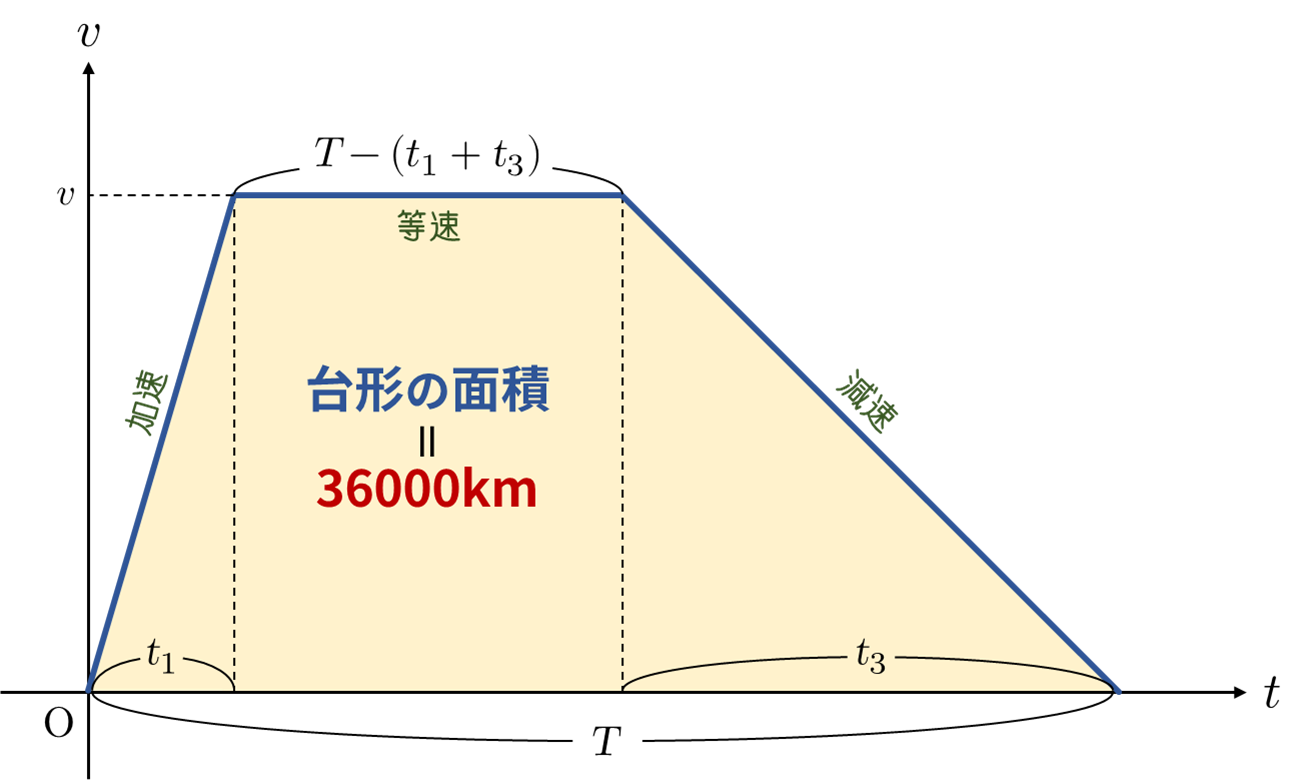
このグラフで囲まれる台形の面積は、エレベーターの移動距離 $36000 \ [\mathrm{km}]$ を表すので、総移動時間を $T \ [\mathrm{s}]$ とすると
$$\begin{eqnarray}
\underbrace{ \{ T-(t_1+t_3)+T \} }_{ \text{(上底+下底)} } \times \underbrace{ v }_{ \text{高さ} } \times \dfrac{1}{2} &=& 36000 \times 10^3 \\
\{ T-(100+1000)+T \} \times 98 \times \dfrac{1}{2} &=& 36000000
\end{eqnarray}$$

$$\begin{eqnarray}
T &=& 367896.9 \\
&=& 367897 \ [\mathrm{s}] \\
&=& \mathbf{102 \ [h] \ 11 \ [m] \ 37 \ [s]}
\end{eqnarray}$$

まとめ

今回は、「高校生クイズ」で出題された、宇宙エレベーターの移動時間を求める計算問題にチャレンジしてみました。

結論は102時間11分37秒、、いつかはこんな乗り物が実現する日が来るのでしょうか。楽しみですね！