今回は、大阪大学物理(2022年〔1〕)の解説をしたいと思います。
前文
図 $1$ のように,水平方向に $x$ 軸,鉛直上向きに $y$ 軸をとった平面内における質量 $M$ の物体 $\mathrm{A}$ と質量 $m$ の物体 $\mathrm{B}$ の運動を考える。物体 $\mathrm{A}$ は,$x$ 軸に平行に固定された棒に沿って滑らかに動くことができる。また,物体 $\mathrm{A}$ と物体 $\mathrm{B}$ は伸び縮みしない長さ $\ell$ で質量の無視できる糸でつながれている。糸と鉛直方向のなす角度 $\theta$〔$\mathrm{rad}$〕を,図 $1$ に示すように定義する。物体 $\mathrm{A}$ と棒の間の摩擦力は無視でき,また,物体 $\mathrm{A}$ および物体 $\mathrm{B}$ は質点とみなしてよい。重力加速度の大きさを $g$ とする。
(大阪大学)
Ⅰ.
問題
まず,物体 $\mathrm{A}$ を棒の一点に動かないように固定する。糸がたるまないように物体 $\mathrm{B}$ を持ち上げ,静かに離すと物体 $\mathrm{B}$ は振動をはじめた。このとき,以下の問に答えよ。
問1 以下の文中の空欄に入れるべき数式を解答欄に記せ。
糸の角度が $\theta$ のとき,糸の張力の大きさを $S$,物体 $\mathrm{B}$ の加速度の $x$ 成分および $y$ 成分を,それぞれ,$a_x$ および $a_y$ とするとき,物体 $\mathrm{B}$ の運動方程式は,$ma_x=\bbox[3px,border: 2px solid]{~~~~\text{⒜}~~~~}$ および $ma_y=\bbox[3px,border: 2px solid]{~~~~\text{⒝}~~~~}$ と表される。問2 $|\theta|$ が十分に小さいとき,物体 $\mathrm{B}$ は水平方向にのみ運動すると考えてよい。このとき,問 $1$ で求めた運動方程式において,$\sin\theta \fallingdotseq \theta$,$\cos\theta \fallingdotseq 1$ と近似し,振動の周期 $T$ を求めよ。
(大阪大学)
解答
問1
物体 $\mathrm{B}$ が図 $1$ の位置にあるときに働く力の大きさは
$$\begin{align}
x \ \text{軸方向:}&\text{左向きに} \ S\sin\theta \\
y \ \text{軸方向:}&\text{上向きに} \ S\cos\theta \ \text{、下向きに} \ mg
\end{align}$$であるから、軸の正の向きと力の方向に注意すると
$$\begin{eqnarray}
ma_x &=& \bbox[6px,border: 2px solid]{-S\sin\theta}_\text{ ⒜} \quad \cdots \text{①} \\
ma_y &=& \bbox[6px,border: 2px solid]{S\cos\theta -mg}_\text{ ⒝} \quad \cdots \text{②}
\end{eqnarray}$$
問2
①,②において $\sin\theta \fallingdotseq \theta$,$\cos\theta \fallingdotseq 1$ と近似すると
$$\begin{eqnarray}
ma_x &=& -S\theta \quad\cdots\text{③} \\
ma_y &=& S-mg \quad\cdots\text{④}
\end{eqnarray}$$となる。
物体 $\mathrm{B}$ が水平方向にのみ運動すると考えると、鉛直方向の力は釣り合っているから、④より
$$ma_y=S-mg=0 \ \Longleftrightarrow \ S=mg\quad\cdots\text{⑤}$$となり、⑤を③に代入すると
$$\begin{eqnarray}
ma_x &=& -mg\theta \\
\therefore\quad a_x &=& -g\theta\quad\cdots\text{⑥}
\end{eqnarray}$$が成り立つ。
ここで、物体 $\mathrm{B}$ が水平方向右向きに $x$ だけ移動した位置にあるとき、
$$\begin{eqnarray}
x &=& \ell\sin\theta\fallingdotseq\ell\theta \\
\therefore\quad\theta &=& \dfrac{x}{\ell}
\end{eqnarray}$$であるから、これを⑥に代入すると
$$a_x=-\dfrac{g}{\ell}x\quad\cdots\text{⑦}$$となる。単振動の角速度を $\omega$ とすると、$a_x=-\omega^2x$ と⑦より
$$\omega=\sqrt{\dfrac{g}{\ell}}$$
よって
$$T=\dfrac{2\pi}{\omega}=\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{2\pi\sqrt{\dfrac{\ell}{g}}}}$$
Ⅱ.
問題
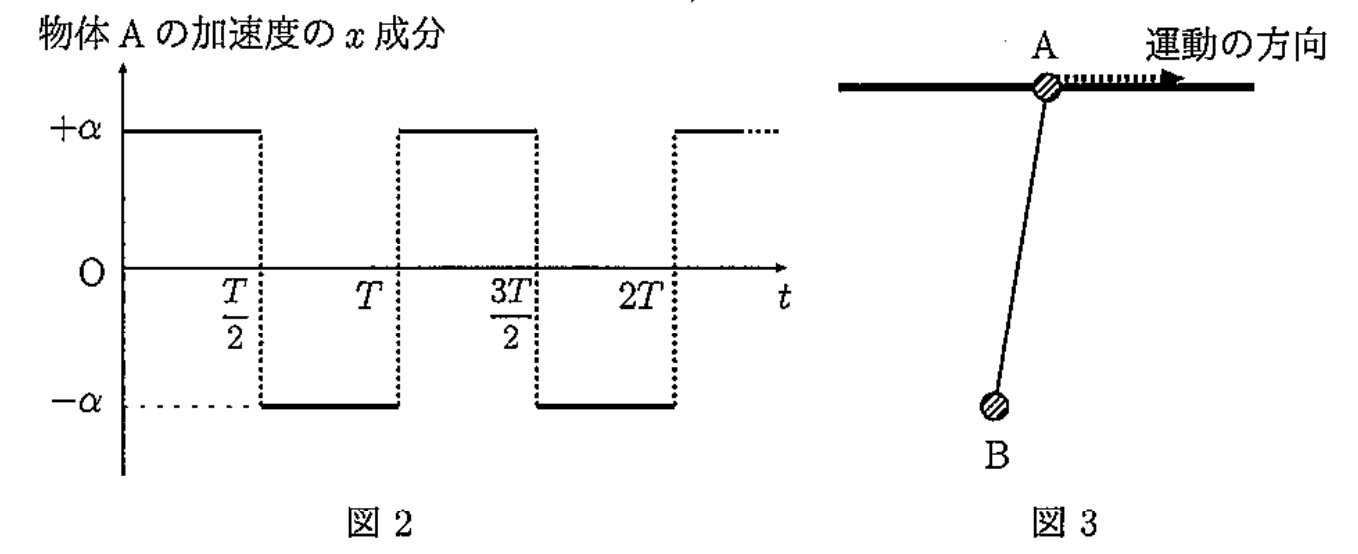
次に,物体 $\mathrm{A}$ を棒に沿って動かす。ただし,物体 $\mathrm{A}$ の加速度の $x$ 成分が,図 $2$ に示すように,$\dfrac{T}{2}$ ごとに $\pm\alpha$( $\alpha \gt 0$ )で符号が変わるように物体 $\mathrm{A}$ を加減速させながら動かす。ここで,$T$ は問 $2$ で求めた周期である。また,時刻 $t=0$ で糸は鉛直で,物体はいずれも静止しており,このときの物体の位置の $x$ 座標を $0$ とする。なお,物体 $\mathrm{B}$ の振動の周期は十分小さく,$|\theta|$ は十分に小さいとしてよい。この時,以下の問に答えよ。
問3 時刻 $t=nT$( $n$ は自然数)における物体 $\mathrm{A}$ の $x$ 座標 $x_n$ を求めよ。
問4 時刻 $t$ が $0\lt t\lt \dfrac{T}{2}$ の間の運動を考える(図 $3$ )。このとき,以下の文中の空欄に入れるべき数式を解答欄に記せ。
物体 $\mathrm{A}$ とともに動く非慣性系で物体 $\mathrm{B}$ に作用する慣性力の水平成分は,右向きを正として $\bbox[3px,border: 2px solid]{~~~~\text{⒞}~~~~}$ であるので,この非慣性系で,物体 $\mathrm{B}$ は初期位置から水平方向に右向きを正として,$\bbox[3px,border: 2px solid]{~~~~\text{⒟}~~~~}$ だけずれた位置を中心として,周期が $T$ の単振動を半周期だけする。したがって,時刻 $t=\dfrac{T}{2}$ で,糸の角度 $\theta$ は $\bbox[3px,border: 2px solid]{~~~~\text{⒠}~~~~}$ となり,この非慣性系で物体 $\mathrm{B}$ は静止する。ただし,角度 $\theta$ は図 $1$ のように定義する。問5 時刻 $t=nT$( $n$ は自然数)における糸の角度 $\theta_n$ を求めよ。
問6 物体 $\mathrm{A}$ が図 $2$ に示す加速度の $x$ 成分をもつためには,物体 $\mathrm{A}$ に重力,糸からの張力,棒からの抗力以外に,外力を作用させる必要がある。$t=\dfrac{T}{6}$ におけるこの外力の $x$ 成分を求めよ。
(大阪大学)
解答
問3
時刻 $t$ における物体 $\mathrm{A}$ の速度の $x$ 成分を $v(t)$ とする。
加速度を $t$ 軸に沿って積分すると速度になるので、
$$v(0)=0, \quad v\left(\dfrac{T}{2}\right)=\dfrac{\alpha T}{2}, \quad v(T)=0$$となり、$0 \leqq t \leqq \dfrac{T}{2}$,$\dfrac{T}{2} \leqq t \leqq T$ における速度はそれぞれ直線的に変化する。また、この変化を $t \geqq T$ において繰り返す。
同様に、速度を $t$ 軸に沿って積分すると変位になるので、$t=T$ における物体 $\mathrm{A}$ の $x$ 座標は
$$\dfrac{1}{2}\cdot T\cdot \dfrac{\alpha T}{2} = \dfrac{\alpha T^2}{4}$$となる。以降、時刻 $T$ ごとに $x$ 座標は $\dfrac{\alpha T^2}{4}$ ずつ増加する。
よって
$$x_n=\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{n\alpha T^2}{4}}}$$
問4
慣性力の向きは加速度の向きと反対であり、$0\lt t\lt \dfrac{T}{2}$ における物体 $\mathrm{A}$ の加速度の $x$ 成分は $+\alpha$ なので、物体 $\mathrm{B}$ に作用する慣性力の水平成分は $\bbox[6px,border: 2px solid]{-m\alpha}_\text{ ⒞}$
物体 $\mathrm{B}$ に作用する重力 $mg$、慣性力 $m\alpha$、糸の張力 $S_1$ が釣り合うとき、非慣性系で物体 $\mathrm{B}$ が水平方向右向きに $x_0$ だけずれた位置にあるとすると、
$$x_0=-\dfrac{\ell\alpha}{g}$$となる。
一方、非慣性系での物体 $\mathrm{B}$ の変位を $x$ とすると、
$$ma_x=-m\alpha-mg\theta=-m\alpha-\dfrac{mg}{\ell}x=-\dfrac{mg}{\ell}(x-x_0)$$となり、合力 $ma_x$ が常に釣り合いの位置( $x=x_0$ )を向くことが分かるので、物体 $\mathrm{B}$ の単振動の中心は初期位置から $\bbox[6px,border: 2px solid]{-\dfrac{\ell\alpha}{g}}_\text{ ⒟}$ だけずれた位置である。
単振動を半周期だけした物体 $\mathrm{B}$ は、非慣性系で振動中心を軸として反対側まで運動するので、時刻 $t=\dfrac{T}{2}$ における糸の角度を $\theta$ とすると、
$$\begin{eqnarray}
\ell\theta &=& 2\cdot\left(-\dfrac{\ell\alpha}{g}\right) \\[0.5em]
\therefore\quad \theta &=& \bbox[6px,border: 2px solid]{-\dfrac{2\alpha}{g}}_\text{ ⒠}
\end{eqnarray}$$
問5
問4と同様に考えると、非慣性系で、$\dfrac{T}{2}\lt t \lt T$ における物体 $\mathrm{B}$ の単振動の中心は初期位置から $\dfrac{\ell\alpha}{g}$ だけずれた位置となる。また、この単振動の中心位置の変化を $t \geqq T$ において繰り返す。
よって、非慣性系で、$\dfrac{(n-1)T}{2}\lt t \lt \dfrac{nT}{2}$ における物体 $\mathrm{B}$ の単振動の中心は初期位置から
$$\begin{cases}
-\dfrac{\ell\alpha}{g} & \text{(} \ n \ \text{が奇数のとき)}\quad\cdots\text{⑧} \\
\dfrac{\ell\alpha}{g} & \text{(} \ n \ \text{が偶数のとき)}\quad\cdots\text{⑨} \\
\end{cases}$$だけずれた位置であると分かる。
ここで、時刻 $t=\left(n+\dfrac{1}{2}\right)T$ における糸の角度を $\theta_n’$ とすると、⑧より $\ell\theta_n$ と $\ell\theta_n’$ の中心が $-\dfrac{\ell\alpha}{g}$ なので
$$\begin{align}
\dfrac{\ell\theta_n+\ell\theta_n’}{2}&=-\dfrac{\ell\alpha}{g} \\
\theta_n’&=-\theta_n-\dfrac{2\alpha}{g}
\end{align}$$同様に、⑨より $\ell\theta_n’$ と $\ell\theta_{n+1}$ の中心が $\dfrac{\ell\alpha}{g}$ なので
$$\begin{align}
\dfrac{\ell\theta_n’+\ell\theta_{n+1}}{2}&=\dfrac{\ell\alpha}{g} \\ \theta_{n+1}&=-\theta_n’+\dfrac{2\alpha}{g} \\
&=-\left(-\theta_n-\dfrac{2\alpha}{g}\right)+\dfrac{2\alpha}{g} \\
&=\theta_n+\dfrac{4\alpha}{g}\quad\cdots\text{⑩}
\end{align}$$となり、$\theta_n$ と $\theta_{n+1}$ の間を関係づける漸化式が得られる。
初項 $\theta_1$ は、時刻 $t=T$ における糸の角度なので、
$$\theta_1=\dfrac{\alpha}{g}+\left\{\dfrac{\alpha}{g}-\left(-\dfrac{2\alpha}{g}\right)\right\}=\dfrac{4\alpha}{g}\quad\cdots\text{⑪}$$
したがって、⑩,⑪より、数列 $\{\theta_n\}$ は初項 $\theta_1=\dfrac{4\alpha}{g}$、公差 $\dfrac{4\alpha}{g}$ の等差数列であるから
$$\theta_n=\dfrac{4\alpha}{g}+(n-1)\dfrac{4\alpha}{g}=\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{4n\alpha}{g}}}$$
問6
$0\lt t\lt \dfrac{T}{2}$ における糸の角度を $\theta(t)$ とすると、問4より、$\theta(t)$ のグラフは次のようになる。
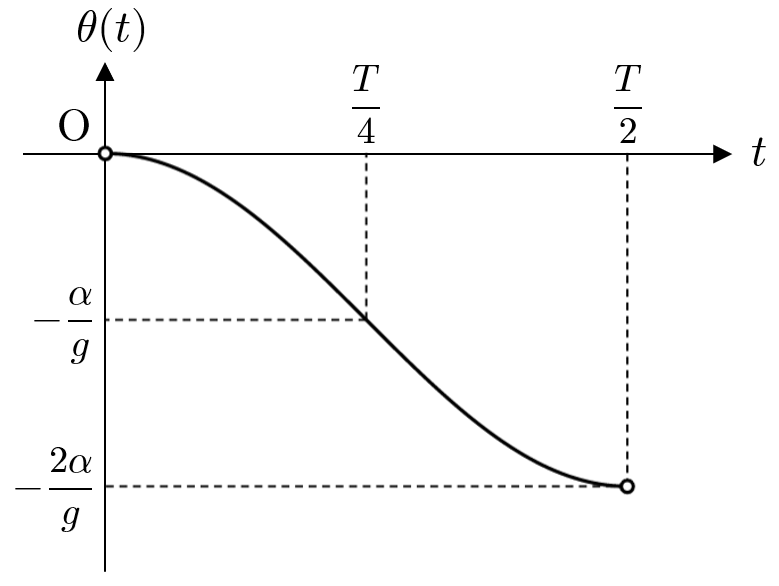
このグラフは、$\theta(t)=\cos t$ のグラフを $x$ 軸方向に $\dfrac{T}{2\pi}$ 倍、$y$ 軸方向に $\dfrac{\alpha}{g}$ 倍し、さらに $y$ 軸方向に $-\dfrac{\alpha}{g}$ だけ平行移動して得られるものなので、
$$\theta(t)=\dfrac{\alpha}{g}\left\{\cos\left(\dfrac{2\pi}{T}t\right)-1\right\}$$と表すことができる。
よって、$t=\dfrac{T}{6}$ のとき
$$\theta\left(\dfrac{T}{6}\right)=\dfrac{\alpha}{g}\left\{\cos\left(\dfrac{2\pi}{T}\cdot\dfrac{T}{6}\right)-1\right\}=-\dfrac{\alpha}{2g}$$
ここで、求める外力の $x$ 成分を $F$ とすると、⑤より、物体 $\mathrm{A}$ は重力 $Mg$、糸からの張力 $mg$、棒からの抗力、外力 $F$ を受けることで右向きに $\alpha$ の加速度が生じている。
糸からの張力 $mg$ の水平成分は
$$mg\sin\left\{\theta\left(\dfrac{T}{6}\right)\right\} \fallingdotseq mg\theta\left(\dfrac{T}{6}\right)=-\dfrac{m\alpha}{2}$$であるから、物体 $\mathrm{A}$ についての水平方向の運動方程式より
$$\begin{align}
M\alpha &= F-\dfrac{m\alpha}{2} \\
\therefore\quad F &= \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\left(M+\dfrac{m}{2}\right)\alpha}}
\end{align}$$
Ⅲ.
問題
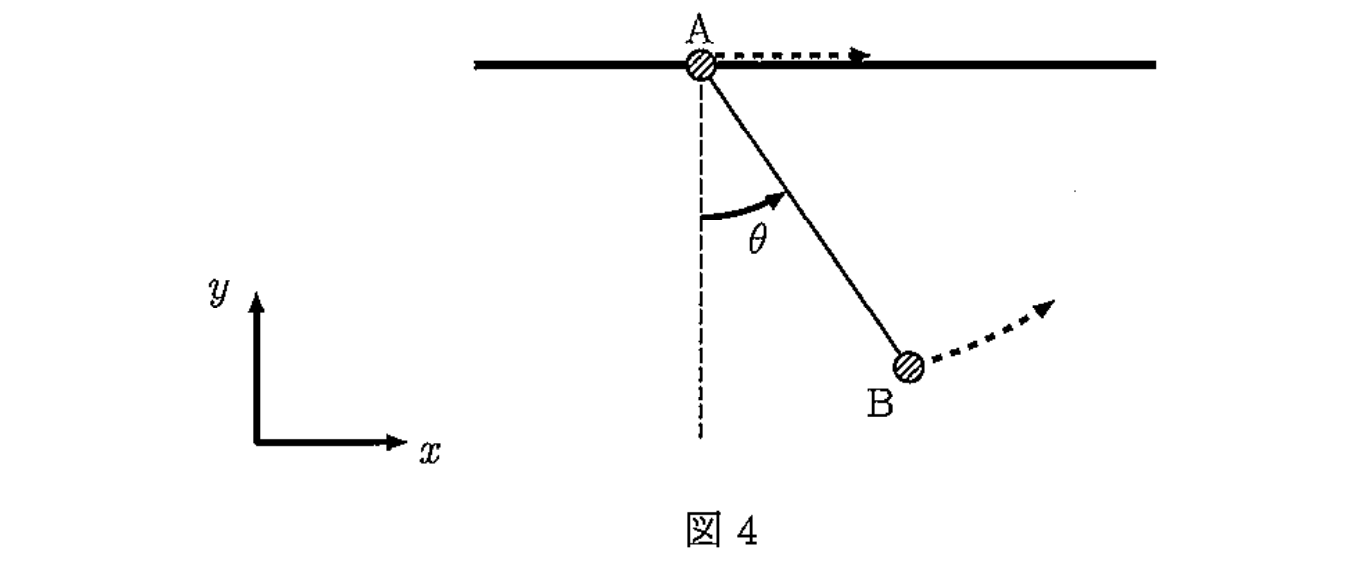
次に,物体 $\mathrm{A}$ を水平な棒に沿って自由に動けるようにする。糸が鉛直で,物体 $\mathrm{A}$ が静止している状態で,物体 $\mathrm{B}$ に $x$ 軸の正の向きに大きさ $v_0$ の速度を与えたところ,糸はたるまずに,また,糸の角度 $\theta$ が $-\dfrac{\pi}{2}\lt\theta\lt\dfrac{\pi}{2}$ のある範囲で,物体 $\mathrm{B}$ は振動した。図 $4$ には,ある時刻における,物体 $\mathrm{A}$ および物体 $\mathrm{B}$ の運動の様子を点線で示す。ただし,$|\theta|$ は微小とは限らない。このとき,以下の問に答えよ。
問7 物体 $\mathrm{B}$ が最高点に達したときの,物体 $\mathrm{A}$ の速さを求めよ。
問8 物体 $\mathrm{B}$ の最高点の高さを,物体 $\mathrm{B}$ の初期位置を基準として求めよ。
(大阪大学)
解答
問7
求める速さを $V$ とすると、物体 $\mathrm{B}$ が最高点に達したとき、物体 $\mathrm{B}$ の速度の鉛直成分は $0$ であるから、物体 $\mathrm{A}$ と 物体 $\mathrm{B}$ は同じ速さ $V$ で運動すると考えられる。
よって、運動量保存則より
$$\begin{align}
mv_0 &= MV+mV \\
\therefore\quad F &= \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{m}{M+m}v_0}}
\end{align}$$
問8
求める高さを $h$ とすると、物体 $\mathrm{A}$ と 物体 $\mathrm{B}$ からなる系についての「運動開始時」と「物体 $\mathrm{B}$ が最高点に達したとき」における力学的エネルギー保存則より
$$\begin{align}
Mg\ell + \dfrac{1}{2}mv_0^2 &= \dfrac{1}{2}MV^2+mg\ell + \dfrac{1}{2}mV^2+mgh \\
mgh &= \dfrac{1}{2}\left\{mv_0^2 \ – \ (M+m)\left(\dfrac{m}{M+m}v_0\right)^2\right\} \\
\therefore\quad h&= \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{Mv_0^2}{2(M+m)g}}}
\end{align}$$
答え一覧
Ⅰ.
$$\begin{align}
\text{問1}&\quad\bbox[3px,border: 2px solid]{~~~~\text{⒜}~~~~}\cdots -S\sin\theta \\[0.5em]
&\quad\bbox[3px,border: 2px solid]{~~~~\text{⒝}~~~~}\cdots S\cos\theta -mg \\[0.5em]
\text{問2}&\quad 2\pi\sqrt{\dfrac{\ell}{g}}
\end{align}$$
Ⅱ.
$$\begin{align}
\text{問3}&\quad \dfrac{n\alpha T^2}{4} \\[0.5em]
\text{問4}&\quad\bbox[3px,border: 2px solid]{~~~~\text{⒞}~~~~}\cdots -m\alpha \\[0.5em]
&\quad\bbox[3px,border: 2px solid]{~~~~\text{⒟}~~~~}\cdots -\dfrac{\ell\alpha}{g} \\[0.5em]
&\quad\bbox[3px,border: 2px solid]{~~~~\text{⒠}~~~~}\cdots -\dfrac{2\alpha}{g} \\[0.5em]
\text{問5}&\quad \dfrac{4n\alpha}{g} \\[0.5em]
\text{問6}&\quad \left(M+\dfrac{m}{2}\right)\alpha
\end{align}$$
Ⅲ.
$$\begin{array}{l}
\text{問7}\quad \dfrac{m}{M+m}v_0 \\[0.5em]
\text{問8}\quad \dfrac{Mv_0^2}{2(M+m)g}
\end{array}$$
まとめ
今回は、大阪大学物理(2022年〔1〕)の解説をしました。