正100角形の対角線は何本？

今回は、正100角形の対角線が何本か計算で求める方法を紹介したいと思います。

記事後半では、一般化（正 $n$ 角形）にもチャレンジしているので、ぜひ最後までご覧ください。

まずは正10角形

いきなり正100角形の対角線を引いて数えるのは無謀なので、辺の数を少なくした正10角形で試してみて、正100角形への手がかりを探っていくことにしましょう。

作図してみよう

正10角形はこんな形です。各頂点に1～10と番号をふってみました。

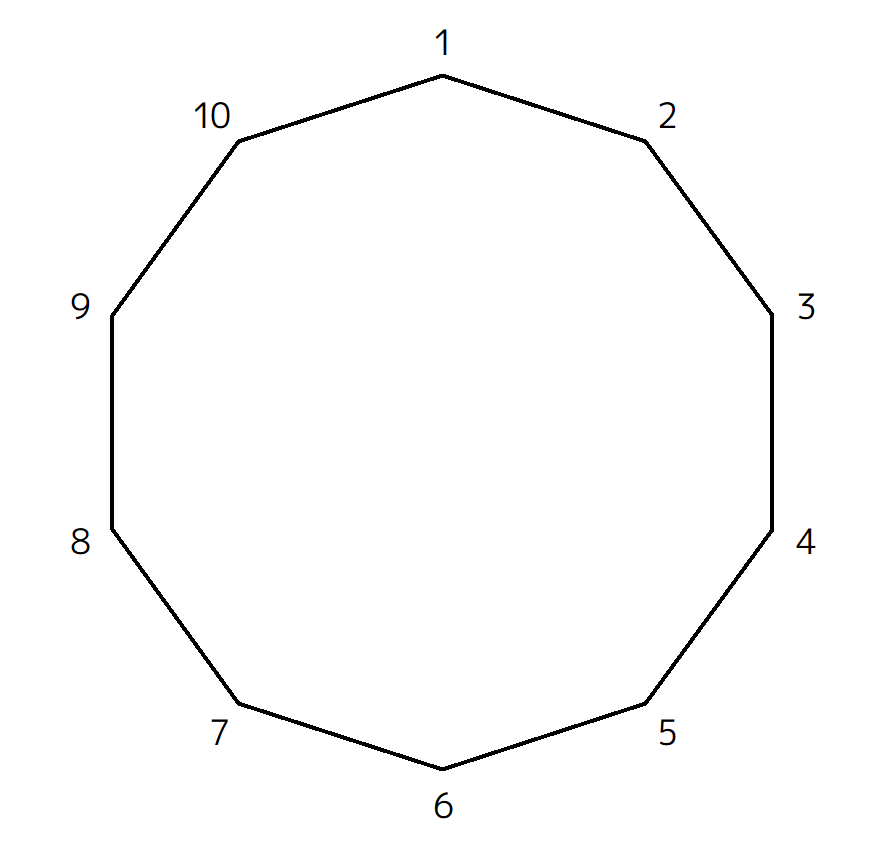
では対角線を引いていきます。
どのように引いても全体の本数は変わりませんが、規則性をつかむために、まずは頂点1から引ける対角線をすべて引いてみましょう。

するとこのように、頂点3～9に向けて7本の対角線が引けます。

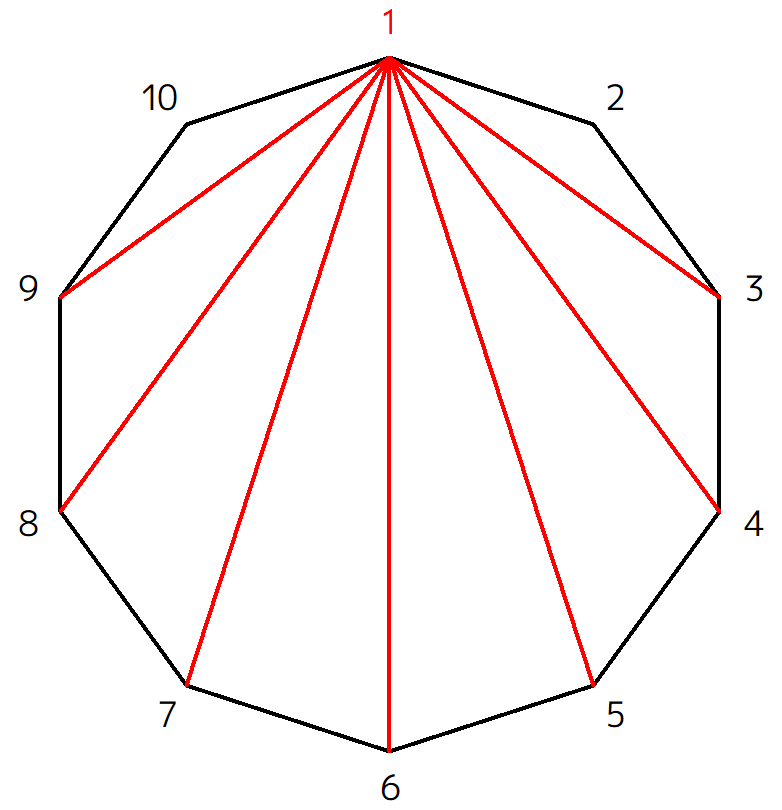
では次に、頂点2から引ける対角線をすべて引いてみましょう。
するとこのように、頂点4～10に向けて7本の対角線が引けます。

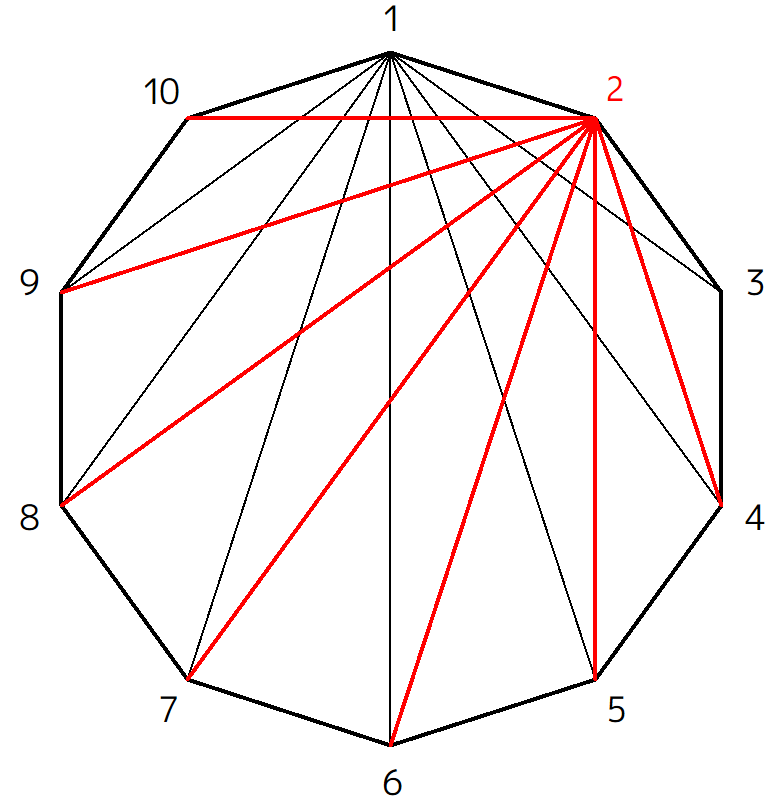
そして同じように頂点3からも引いていきます。
が、ここであることに気がつきます。

そうなんです。そうなんですが、ここはあえて同じところをもう一度引きます。ただし、2回目に引くところ（ここでは1-3間）は青線にして区別します。

するとこのように、頂点1、5～10に向けて7本の対角線（赤6本＋青1本）が引けます。

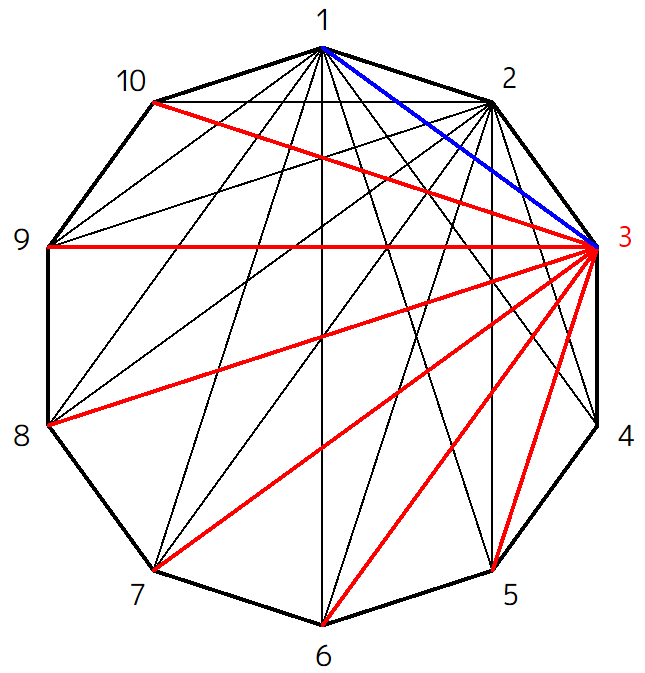
だいぶごちゃごちゃしてきました…。(笑)

この作業を頂点4、5、……と繰り返し、頂点9から引ける対角線を引ききった時点の図がこれです。

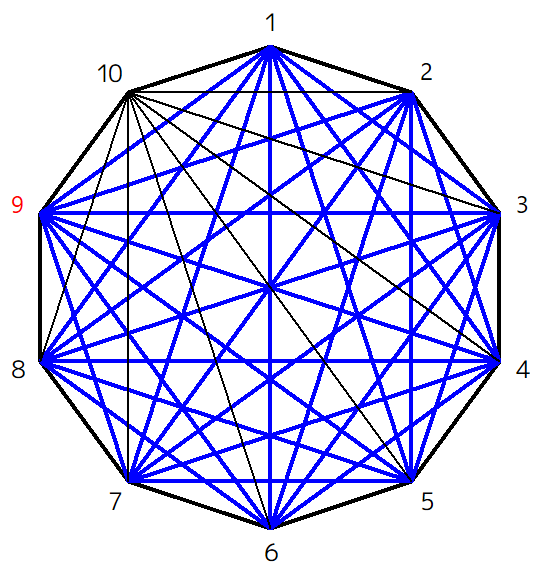
ほとんど真っ青になりました(笑)

最後に頂点10から引きますが、すでに頂点2～8から引かれた黒線ばかりですので、7本とも青線で引きます。

先ほどの図でほとんど完成でしたが、これにて本当に完成です！

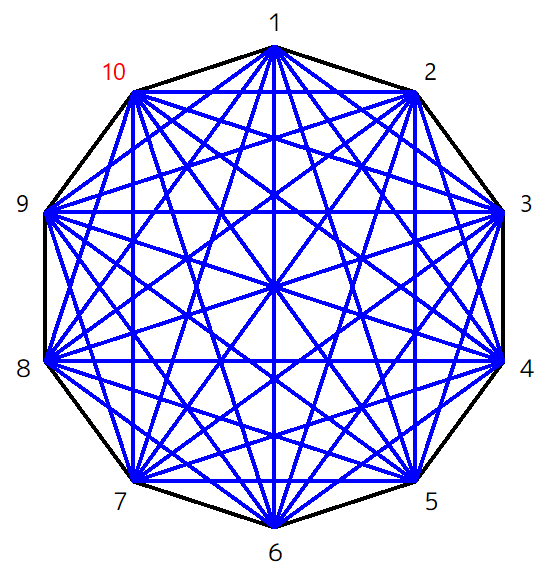
規則性は？

正10角形の対角線をすべて引いてみましたが、結局何本引いたのでしょうか？
実際に数えてみるとわかりますが、全部で35本あります。

ではこの35本、どうにか計算で求められないでしょうか？

――実は求められるんです！
計算で求められるということは何か規則性があるに違いない、、そう感じたあなたは勘が鋭い！

ではその規則性とは何か？この記事のキモはここにあります。

自分で考えたい人は下を読む前に考えてみましょう。

それでは種明かしです。

正10角形の対角線に関する規則性とは、次の2つです。

まず①の「7本」はどこから出てきたのでしょうか？

これは、全10頂点から「対角線を引き始める頂点」と「その両隣の頂点」を引いた数です。

例えば頂点2から対角線を引く場合、自分自身（頂点2）に対角線は引けません。
また、両隣（頂点1、3）にも引けません（すでにそこには図形の辺がありますからね）。
つまり、7＝10－3ということなのです。

では②は具体的には何を意味しているのでしょうか？

これは、どの対角線もちょうど2回引かれたということです。

例えば「1-3間の青線」は「頂点1から3へ向けて引いた線」と「頂点3から1へ向けて引いた線」で2回引かれています。
他の対角線についても同様です。

これら①②を組み合わせると、35本という数字を導くことができます。やってみましょう。

• 頂点1からは7本（＝10－3）の対角線が引ける。頂点2～10からも同様に、それぞれ7本の対角線が引ける。
  つまり重複を許せば、のべ70本（＝7×10）の対角線が引ける。
• それぞれの対角線は2重で引かれているので、実際の対角線の本数はその半分である。
  つまり、70÷2＝35本。

これが対角線の本数に関する規則性だったのです！

いよいよ正100角形！

それではいよいよ本題、正100角形の対角線の本数を数えていきましょう！

といっても考え方や計算方法は先ほどと同じですので、「数える」というよりは「求める」の方がしっくりきますかね(笑)

• 頂点1からは97本（＝100－3）の対角線が引ける。頂点2～100からも同様に、それぞれ97本の対角線が引ける。
  つまり重複を許せば、のべ9700本（＝97×100）の対角線が引ける。
• それぞれの対角線は2重で引かれているので、実際の対角線の本数はその半分である。
  つまり、9700÷2＝4850本。

ということで今回のテーマ「正100角形の対角線は何本？」の答えは4,850本でした！

正10角形で35本でしたので、元の図形の辺の数の増え方（10→100）に比べて、対角線の本数の増え方（35→4850）はかなり急激ですね。

ちなみに、正100角形の対角線をすべて引くと、こんな感じになります。

…とお見せしたかったのですが、何しろ線が多すぎて、つぶれてしまいました。

黒丸でもプラネタリウムでもありませんよ(笑)

拡大してみると、緻密な模様ができているのが分かるかと思います。

一般化してみよう

ここまで来たからには、一般の場合、つまり正 $\boldsymbol{n}$ 角形の対角線の本数を求めてみましょう！

正10角形・正100角形のときと同様に進めていくだけです。

• 頂点1からは $n-3$ (本)の対角線が引ける。頂点2～$n$からも同様に、それぞれ $n-3$ (本)の対角線が引ける。
  つまり重複を許せば、のべ $n(n-3)$ (本)の対角線が引ける。
• それぞれの対角線は2重で引かれているので、実際の対角線の本数はその半分である。
  つまり、$n(n-3) \div 2＝\displaystyle \frac{n(n-3)}{2}$ (本)。

これで一般化もばっちりです！見やすいようにまとめておきましょう。

まとめ

今回は、正100角形の対角線の本数を規則性に着目して求めてみました。

結果は4,850本……手描きじゃ絶対ムリですね。パソコンの時代に生まれて良かった(笑)

また、一般化を行うと、対角線の本数は辺の数の2乗のオーダーであることがわかりました。
正10角形から正100角形にしたときに対角線の本数が急増していたのは、式の上でも確かなことだったんですね。

一見突拍子もない問題でも、規則性に気づけば糸がほぐれるように解決できるというケースが数学にはよくあります。
いい意味で面倒くさがり屋さんになって、効率よく正解の道を探ることが大切ですね。