この記事は、『【麻雀】天和の確率は何パーセント?計算して求めてみた』という記事の補足記事になります。
まだ読んでいない方は、ぜひこちらを先に読んでみてください!
さて、上の記事では、「字牌の有効なパターン数」と「数牌の有効なパターン数」の積によって4面子+雀頭のパターン数を算出し、それをもとに天和の確率を計算しました。
字牌については、刻子(または雀頭)しか作りようがないので、有効なパターン数の計算が比較的簡単でした。
それに対して数牌は、刻子(または雀頭)に加えて順子も作れるので、有効なパターン数が膨大になり、計算も複雑になります。
複雑ゆえ、計算式を省略して答えだけ載せてたんですよね。
今回は、そんな「数牌の有効なパターン数」をどのように求めるのか、その途中式を説明する記事になります。
でも「知りたかった!」という方が1人でもいることを信じて魂込めて書くよ!!
はじめに
説明上の注意
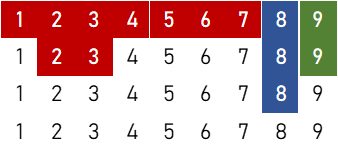
この記事では、牌の並びを説明するものとして下の画像のような図を用います。
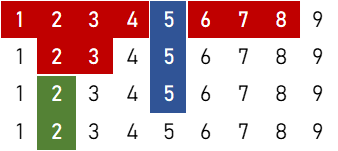
例えば上の図は ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() に対応しています。
に対応しています。
数字だけで説明するよりも視覚的な図があった方が断然分かりやすいですので、これをもとに説明したいと思います。
ただし、いくつか前提・注意点があります。
- 赤色は順子、青色は刻子、緑色は雀頭を表します。
- 順子を含む場合、まず順子の並びを確定させてから、順子→刻子→雀頭の順にマスを埋めるとしてパターン数を計算します。
- 順子が2つ以上の塊に分かれる場合、それらは互いに重なり合わないものとします。
(重なり合う場合、それを1つの塊としたパターン数も別で求めているからです。) - かぶりによる除外の判定をしやすくするため、同列のマスは上から埋めます。
- 確率を計算するためのパターン数を求めるので、同一牌もすべて区別して数えます。
計算例
先ほど挙げた前提・注意点をもとに計算していきますが、文章だけ読んでもイメージがつかないので、簡単な例で練習してみましょう。
数牌5枚の組み合わせのうち、「順子×1+雀頭」のパターン数を数えてみましょう。

この図は ![]()
![]()
![]()
![]()
![]() を表しています。
を表しています。![]()
![]()
![]()
![]()
![]() や
や![]()
![]()
![]()
![]()
![]() など…数えだしたらキリがなさそうですが、一体何通りあるのでしょう?
など…数えだしたらキリがなさそうですが、一体何通りあるのでしょう?
- 「順子×1」の並びは、3連続形(例:


 )で確定しています。
)で確定しています。 - 順子の並びが確定したので、順子を埋めます。
順子の埋め方は [

 ][
][

 ][
][

 ][
][

 ][
][

 ][
][

 ][
][
 ] の $7$ 通りです。
] の $7$ 通りです。 - 次に刻子を埋めますが、今回は刻子が無いので飛ばします。
- 最後に雀頭を埋めます。
ここで、雀頭の埋め方は、すでに埋まっている順子との関係から大きく2種類に分けられます。
順子と別の数字に埋める
(例:順子 [

 ] に対して [
] に対して [
 ] と埋める)
] と埋める)
その埋め方は $6$ 通りです。
順子と同じ数字に埋める
(例:順子 [

 ] に対して [
] に対して [
 ] と埋める)
] と埋める)
その埋め方は $3$ 通りです。 - 以上より、牌の並びを大きく2種類のグループ(・)に分けることができます。
- それぞれに対して「同一牌を区別したパターン数」を求め、足せば完了です。
同一牌を区別するとき、1枚なら ${}_4 \mathrm{C}_1 \ (=4)$ 、2枚なら ${}_4 \mathrm{C}_2 \ (=6)$ 、3枚なら ${}_4 \mathrm{C}_3 \ (=4)$ をかけます。
(0枚や4枚の場合は ${}_4 \mathrm{C}_0 = {}_4 \mathrm{C}_4 =1$ をかけますが、計算に影響しないので式には書きません。)
のグループ

パターン数は$$\begin{eqnarray}
\underbrace{ \color{ #c00000 }{ 7 } }_{ \color{ #c00000 }{ \text{順子} } } \times \underbrace{ \color{ #548235 }{ 6 } }_{ \color{ #548235 }{ \text{雀頭} } } \times \underbrace{ ({}_4 \mathrm{C}_1)^3 }_{ \text{1枚が3種類} } \times \underbrace{ {}_4 \mathrm{C}_2 }_{ \text{2枚が1種類} } \\[0.5em]
= 16,128 \ ( \text{通り} )
\end{eqnarray}$$
のグループ

パターン数は$$\begin{eqnarray}
\underbrace{ \color{ #c00000 }{ 7 } }_{ \color{ #c00000 }{ \text{順子} } } \times \underbrace{ \color{ #548235 }{ 3 } }_{ \color{ #548235 }{ \text{雀頭} } } \times \underbrace{ ({}_4 \mathrm{C}_1)^2 }_{ \text{1枚が2種類} } \times \underbrace{ {}_4 \mathrm{C}_3 }_{ \text{3枚が1種類} } \\[0.5em]
= 1,344 \ ( \text{通り} )
\end{eqnarray}$$
- よって、「順子×1+雀頭」のパターン数は
$$16,128 + 1,344 = 17,472 \ ( \text{通り} )$$

例えばこのパターンはのグループに当てはまり、1パターンとしてきちんと数えられています。
いざ、計算!
数牌0枚
「数牌が1枚もない」という $1 \ ( \text{通り} )$ です。
数牌2枚(雀頭)
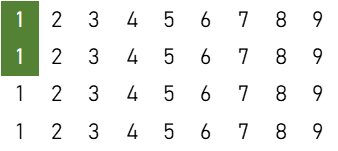
$$9 \times {}_4 \mathrm{C}_2 = 54 \ ( \text{通り} )$$
数牌3枚(1面子)
1刻子
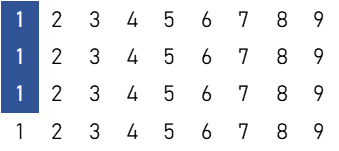
$$9 \times {}_4 \mathrm{C}_3 = 36 \ ( \text{通り} )$$
1順子

$$7 \times ({}_4 \mathrm{C}_1)^3 = 448 \ ( \text{通り} )$$
数牌3枚の有効なパターン数は
$$36 + 448 = 484 \ ( \text{通り} )$$
数牌5枚(1面子+雀頭)
1刻子+雀頭
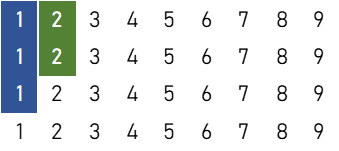
$$9 \times 8 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 = 1,728 \ ( \text{通り} )$$
1順子+雀頭

$$7 \times \{ 6 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 + 3 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_3 \} = 17,472 \ ( \text{通り} )$$
数牌5枚の有効なパターン数は
$$1,728 + 17,472 = 19,200 \ ( \text{通り} )$$
数牌6枚(2面子)
2刻子
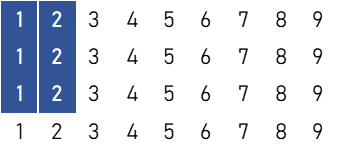
$${}_9 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 576 \ ( \text{通り} )$$
1刻子+1順子

$$7 \times \{ 6 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_1)^2 \} = 11,088 \ ( \text{通り} )$$
2順子
①

$${}_5 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_1 )^6 = 40,960 \ ( \text{通り} )$$
②
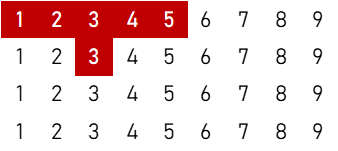
$$5 \times ( {}_4 \mathrm{C}_1 )^4 \times {}_4 \mathrm{C}_2 = 7,680 \ ( \text{通り} )$$
③

$$6 \times ( {}_4 \mathrm{C}_1 )^2 \times ( {}_4 \mathrm{C}_2 )^2 = 3,456 \ ( \text{通り} )$$
④

$$7 \times ( {}_4 \mathrm{C}_2 )^3 = 1,512 \ ( \text{通り} )$$
$53,608 \ ( \text{通り} )$
数牌6枚の有効なパターン数は
$$576+11,088+53,608 = 65,272 \ ( \text{通り} )$$
数牌8枚(2面子+雀頭)
2刻子+雀頭
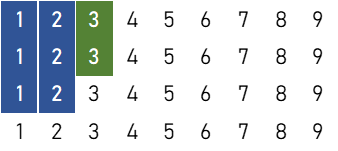
$${}_9 \mathrm{C}_2 \times 7 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 24,192 \ ( \text{通り} )$$
1刻子+1順子+雀頭

$$\begin{eqnarray}
7 \times [ 6 \times \{ 5 \times ( {}_4 \mathrm{C}_1 )^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 3 \times ( {}_4 \mathrm{C}_1 )^2 \times ( {}_4 \mathrm{C}_3 )^2 \} \\
+ 3 \times \{ 6 \times ( {}_4 \mathrm{C}_1 )^2 \times {}_4 \mathrm{C}_2 + 2 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_3 \} ] \\
= 367,584 \ ( \text{通り} )
\end{eqnarray}$$
2順子+雀頭
①
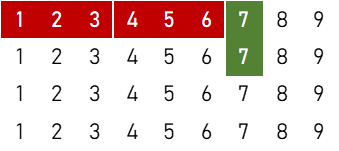
$${}_5 \mathrm{C}_2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_2 +6 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_3 \} = 983,040 \ ( \text{通り} )$$
②
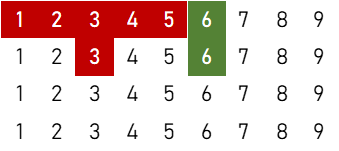
$$5 \times \{ 4 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 + 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 1 \times ({}_4 \mathrm{C}_1)^4 \} = 216,320 \ ( \text{通り} )$$
③

$$6 \times \{ 5 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \} = 111,744 \ ( \text{通り} )$$
④

$$7 \times \{ 6 \times ({}_4 \mathrm{C}_2)^4 + 3 \times ({}_4 \mathrm{C}_2)^2 \} = 55,188 \ ( \text{通り} )$$
$1,366,292 \ ( \text{通り} )$
かぶりによる除外
「1刻子+1順子+雀頭」どうし
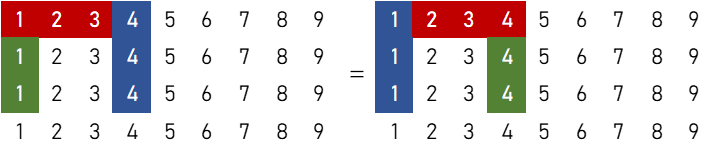
$$6 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^2 = 1,536 \ ( \text{通り} )$$
「2順子+雀頭④」どうし

$$6 \times ({}_4 \mathrm{C}_2)^4 = 7,776 \ ( \text{通り} )$$
$9,312 \ ( \text{通り} )$
数牌8枚の有効なパターン数は
$$24,192+367,584+1,366,292-9,312 = 1,748,756 \ ( \text{通り} )$$
数牌9枚(3面子)
3刻子

$${}_9 \mathrm{C}_3 \times ( {}_4 \mathrm{C}_3 )^3 = 5,376 \ ( \text{通り} )$$
2刻子+1順子

$$7 \times \{ {}_6 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_3)^2 + 6 \times 3 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_3 + {}_3 \mathrm{C}_2 \times {}_4 \mathrm{C}_1 = 115,668 \ ( \text{通り} ) \}$$
1刻子+2順子
①
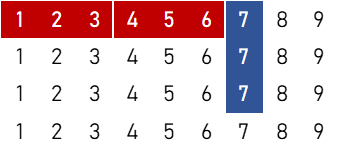
$${}_5 \mathrm{C}_2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_3 +6 \times ({}_4 \mathrm{C}_1)^5 \} = 552,960 \ ( \text{通り} )$$
②
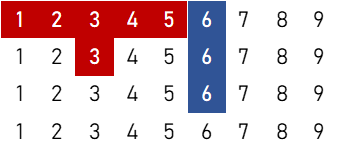
$$5 \times \{ 4 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \} = 130,560 \ ( \text{通り} )$$
③

$$6 \times \{ 5 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \} = 70,848 \ ( \text{通り} )$$
④
$$7 \times 6 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 = 36,288 \ ( \text{通り} )$$
$790,656 \ ( \text{通り} )$
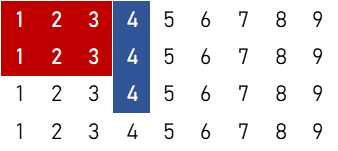
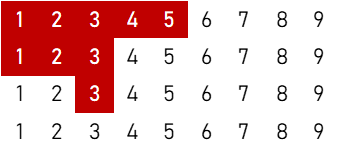
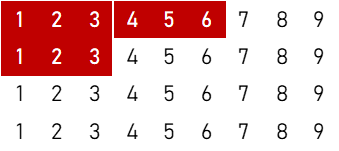
3順子
①

$$7 \times ({}_4 \mathrm{C}_3)^3 = 448 \ ( \text{通り} )$$
②(左右対称含む)

$$6 \times 2 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 = 4,608 \ ( \text{通り} )$$
③(左右対称含む)
$$5 \times 2 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 = 23,040 \ ( \text{通り} )$$
④
$${}_5 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^3 = 276,480 \ ( \text{通り} )$$
⑤

$$5 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 = 11,520 \ ( \text{通り} )$$
⑥(左右対称含む)

$$4 \times 2 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^3 = 110,592 \ ( \text{通り} )$$
⑦

$${}_4 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^2 = 442,368 \ ( \text{通り} )$$
⑧

$$3 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^2 = 110,592 \ ( \text{通り} )$$
⑨
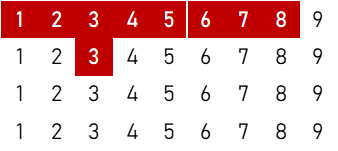
$${}_3 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^7 \times {}_4 \mathrm{C}_2 = 589,824 \ ( \text{通り} )$$
⑩

$$1 \times ({}_4 \mathrm{C}_1)^9 = 262,144 \ ( \text{通り} )$$
$1,831,616 \ ( \text{通り} )$
かぶりによる除外
「3刻子」と「3順子①」

$$7 \times ({}_4 \mathrm{C}_3)^3 = 448 \ ( \text{通り} )$$
数牌9枚の有効なパターン数は
$$5,376+115,668+790,656+1,831,616-448 = 2,742,868 \ ( \text{通り} )$$
数牌11枚(3面子+雀頭)
3刻子+雀頭
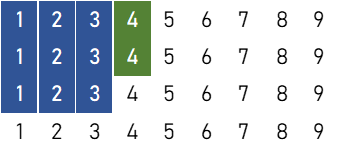
$${}_9 \mathrm{C}_3 \times 6 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 = 193,536 \ ( \text{通り} )$$
2刻子+1順子+雀頭

$$\begin{eqnarray}
7 \times [ {}_6 \mathrm{C}_2 \times \{ 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^3 \} \\
+ 6 \times 3 \times \{ 5 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_3)^2 \} \\
+ {}_3 \mathrm{C}_2 \times \{ 6 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 +1 \times {}_4 \mathrm{C}_3 \} ] \\
= 3,164,196 \ ( \text{通り} )
\end{eqnarray}$$
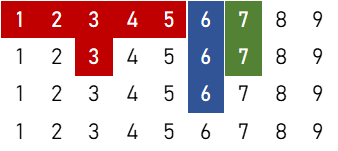
1刻子+2順子+雀頭
①
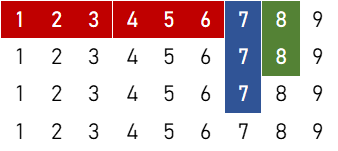
$${}_5 \mathrm{C}_2 \times [ 3 \times \{ 2 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 6 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_3)^2 \} + 6 \times \{ 3 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_2 + 5 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_3 \} ] = 10,260,480 \ ( \text{通り} )$$
②
$$5 \times [ 4 \times \{ 3 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 + 1 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_3 \} + 4 \times \{ 4 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^2 + 3 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 1 \times ({}_4 \mathrm{C}_1)^3 \} ] = 2,932,480 \ ( \text{通り} )$$
③

$$6 \times [ 5 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 \} + 2 \times \{ 5 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^3 + 1 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 \} ] = 1,874,304 \ ( \text{通り} )$$
④

$$7 \times [ 6 \times \{ 5 \times ({}_4 \mathrm{C}_2)^4 \times {}_4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 \} ] = 1,106,784 \ ( \text{通り} )$$
$16,174,048 \ ( \text{通り} )$
3順子+雀頭
①

$$7 \times 6 \times {}4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 = 16,128 \ ( \text{通り} )$$
②(順子の左右対称含む)
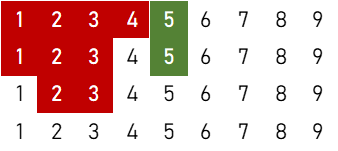
$$6 \times 2 \times \{ 5 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 1 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 + 1 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_3)^2 \} = 143,616 \ ( \text{通り} )$$
③(順子の左右対称含む)
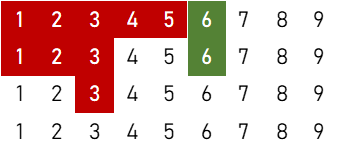
$$5 \times 2 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 \} = 606,720 \ ( \text{通り} )$$
④
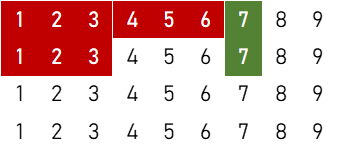
$${}_5 \mathrm{P}_2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^4 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^2 \} = 5,944,320 \ ( \text{通り} )$$
⑤
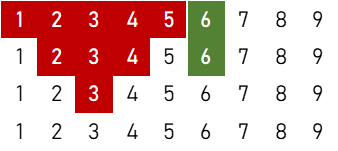
$$5 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 \} = 303,360 \ ( \text{通り} )$$
⑥(順子の左右対称含む)
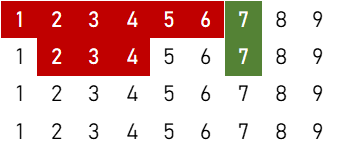
$$4 \times 2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^4 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^2 \} = 2,377,728 \ ( \text{通り} )$$
⑦
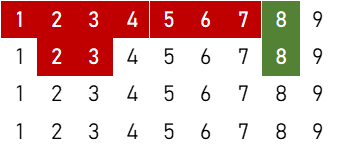
$${}_4 \mathrm{P}_2 \times \{ 2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^3 + 5 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_2 \} = 7,667,712 \ ( \text{通り} )$$
⑧

$$3 \times \{ 2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^3 + 5 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_2 \} = 1,916,928 \ ( \text{通り} )$$
⑨
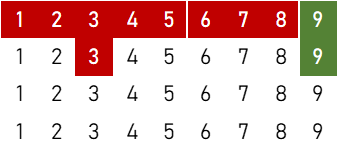
$${}_3 \mathrm{P}_2 \times \{ 1 \times ({}_4 \mathrm{C}_1)^7 \times ({}_4 \mathrm{C}_2)^2 + 7 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 1 \times ({}_4 \mathrm{C}_1)^7 \} = 7,766,016 \ ( \text{通り} )$$
⑩

$$1 \times 9 \times ({}_4 \mathrm{C}_1)^8 \times {}_4 \mathrm{C}_3 = 2,359,296 \ ( \text{通り} )$$
$29,101,824 \ ( \text{通り} )$
かぶりによる除外
「3刻子+雀頭」と「3順子+雀頭①」

$$7 \times 6 \times {}4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 = 16,128 \ ( \text{通り} )$$
「3刻子+雀頭」と「3順子+雀頭②」
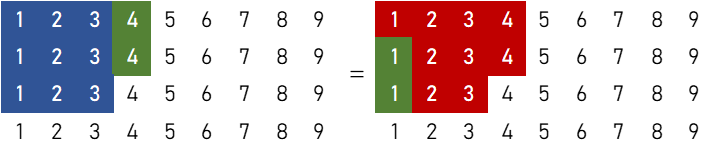
$$6 \times 2 \times {}4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 = 4,608 \ ( \text{通り} )$$
「2刻子+1順子+雀頭」どうし
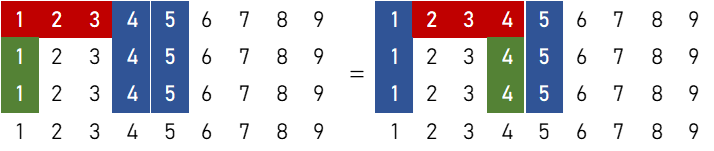
$$6 \times { 5 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^3 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_3)^2 } = 31,488 \ ( \text{通り} )$$
「1刻子+2順子+雀頭①」どうし(その1)
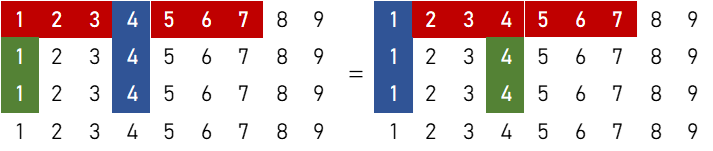
$${}_4 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_3)^2 = 196,608 \ ( \text{通り} )$$
「1刻子+2順子+雀頭①」どうし(その2)
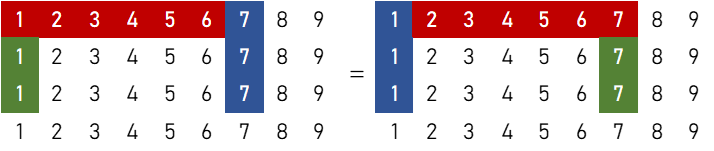
$$3 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_3)^2 = 49,152 \ ( \text{通り} )$$
「1刻子+2順子+雀頭①」と「同②」

$$4 \times 2 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_3 = 8,192 \ ( \text{通り} )$$
「1刻子+2順子+雀頭②」と「同③」

$$5 \times 2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 = 3,840 \ ( \text{通り} )$$
「1刻子+2順子+雀頭③」と「同④」
$$6 \times 2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 = 1,728 \ ( \text{通り} )$$
「1刻子+2順子+雀頭④」どうし

$${}_6 \mathrm{P}_2 \times ({}_4 \mathrm{C}_2)^4 \times {}_4 \mathrm{C}_3 = 155,520 \ ( \text{通り} )$$
「3順子+雀頭②」と「同③」

$$5 \times 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 = 23,040 \ ( \text{通り} )$$
「3順子+雀頭③」と「同④」

$$4 \times 2 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 = 110,592 \ ( \text{通り} )$$
「3順子+雀頭④」どうし

$${}_4 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^4 = 995,328 \ ( \text{通り} )$$
$1,596,224 \ ( \text{通り} )$
数牌11枚の有効なパターン数は
$$193,536+3,164,196+16,174,048+29,101,824-1,596,224 = 47,041,988 \ ( \text{通り} )$$
数牌12枚(4面子)
4刻子
$${}_9 \mathrm{C}_4 \times ( {}_4 \mathrm{C}_3 )^4 = 32,256 \ ( \text{通り} )$$
3刻子+1順子

$$7 \times \{ {}_6 \mathrm{C}_3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_3)^3 + {}_6 \mathrm{C}_2 \times 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^2 + 6 \times {}_3 \mathrm{C}_2 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_3 + 1 \times 1 \} = 656,103 \ ( \text{通り} )$$
2刻子+2順子
①
$${}_5 \mathrm{C}_2 \times \{ {}_3 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^6 \times ({}_4 \mathrm{C}_3)^2 + 3 \times 6 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_3 + {}_6 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^4 \} = 2,741,760 \ ( \text{通り} )$$
②
$$5 \times \{ {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 + 4 \times 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \} = 863,040 \ ( \text{通り} )$$
③

$$6 \times \{ {}_5 \mathrm{C}_2 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 5 \times 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 1 \times ({}_4 \mathrm{C}_2)^2 \} = 587,736 \ ( \text{通り} )$$
④

$$7 \times {}_6 \mathrm{C}_2 \times ({}_4 \mathrm{C}_2)^3 \times ({}_4 \mathrm{C}_3)^2 = 362,880 \ ( \text{通り} )$$
$4,555,416 \ ( \text{通り} )$
1刻子+3順子
①

$$7 \times 6 \times ({}_4 \mathrm{C}_3)^4 = 10,752 \ ( \text{通り} )$$
②(順子の左右対称含む)

$$6 \times 2 \times \{ 5 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 + 1 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 \} = 93,312 \ ( \text{通り} )$$
③(順子の左右対称含む)
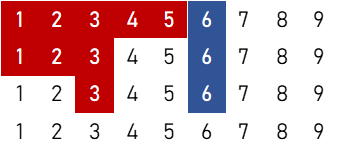
$$5 \times 2 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 \} = 380,160 \ ( \text{通り} )$$
④
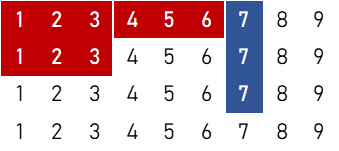
$${}_5 \mathrm{P}_2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^3 \times {}4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \} = 3,525,120 \ ( \text{通り} )$$
⑤

$$5 \times 2 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 \} = 190,080 \ ( \text{通り} )$$
⑥(順子の左右対称含む)
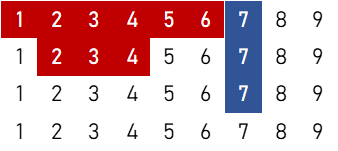
$$4 \times 2 \times \{ 3 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_2)^3 \} = 1,410,048 \ ( \text{通り} )$$
⑦
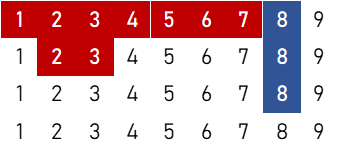
$${}_4 \mathrm{P}_2 \times \{ 2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^2 \times {}4 \mathrm{C}_3 + 5 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 \} = 4,091,904 \ ( \text{通り} )$$
⑧

$$3 \times \{ 2 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 5 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_2)^2 \} = 1,022,976 \ ( \text{通り} )$$
⑨

$${}_3 \mathrm{P}_2 \times \{ 1 \times ({}_4 \mathrm{C}_1)^7 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 7 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_2 \} = 3,391,488 \ ( \text{通り} )$$
⑩

$$1 \times 9 \times ({}_4 \mathrm{C}_1)^8 = 589,824 \ ( \text{通り} )$$
$14,705,664 \ ( \text{通り} )$
4順子

| 番号 | 順子並び | 左右対称 | 1段 | 2段 | 3段 | パターン数 |
| ① | 7 | 1 | 0 | 0 | 0 | 7 |
| ② | 6 | 2 | 1 | 0 | 1 | 192 |
| ③ | 5 | 2 | 2 | 0 | 2 | 2,560 |
| ④ | 20 | 1 | 3 | 0 | 3 | 81,920 |
| ⑤ | 6 | 1 | 0 | 2 | 0 | 216 |
| ⑥ | 5 | 2 | 1 | 2 | 1 | 5,760 |
| ⑦ | 4 | 2 | 2 | 2 | 2 | 73,728 |
| ⑧ | 12 | 1 | 4 | 1 | 2 | 294,912 |
| ⑨ | 5 | 1 | 0 | 4 | 0 | 6,480 |
| ⑩ | 4 | 2 | 1 | 4 | 1 | 165,888 |
| ⑪ | 3 | 2 | 3 | 3 | 1 | 331,776 |
| ⑫ | 6 | 1 | 5 | 2 | 1 | 884,736 |
| ⑬ | 10 | 1 | 0 | 6 | 0 | 466,560 |
| ⑭ | 12 | 1 | 2 | 5 | 0 | 1,492,992 |
| ⑮ | 6 | 1 | 4 | 4 | 0 | 1,990,656 |
| ⑯ | 3 | 1 | 6 | 3 | 0 | 2,654,208 |
| ⑰ | 5 | 1 | 2 | 0 | 2 | 1,280 |
| ⑱ | 4 | 2 | 3 | 0 | 3 | 32,768 |
| ⑲ | 12 | 1 | 4 | 1 | 2 | 294,912 |
| ⑳ | 4 | 1 | 2 | 2 | 2 | 36,864 |
| ㉑ | 3 | 2 | 3 | 3 | 1 | 331,776 |
| ㉒ | 6 | 1 | 5 | 2 | 1 | 884,736 |
| ㉓ | 3 | 1 | 2 | 5 | 0 | 373,248 |
| ㉔ | 2 | 2 | 4 | 4 | 0 | 1,327,104 |
| ㉕ | 1 | 2 | 6 | 3 | 0 | 1,769,472 |
| ㉖ | 3 | 1 | 4 | 4 | 0 | 995,328 |
| ㉗ | 2 | 1 | 6 | 3 | 0 | 1,769,472 |
| ㉘ | 3 | 1 | 4 | 1 | 2 | 73,728 |
| ㉙ | 6 | 1 | 5 | 2 | 1 | 884,736 |
| ㉚ | 2 | 1 | 4 | 4 | 0 | 663,552 |
| ㉛ | 1 | 2 | 6 | 3 | 0 | 1,769,472 |
| ㉜ | 1 | 1 | 6 | 3 | 0 | 884,736 |
| 合計 | 20,545,775 | |||||
「パターン数」=「順子並び」×「左右対称」×「1段」×${}_4 \mathrm{C}_1$×「2段」×${}_4 \mathrm{C}_2$×「3段」×${}_4 \mathrm{C}_3$
かぶりによる除外
「4刻子」と「1刻子+3順子①」

$$7 \times 6 \times ({}_4 \mathrm{C}_3)^4 = 10,752 \ ( \text{通り} )$$
「3刻子+1順子」と「4順子①」

$$7 \times 1 = 7 \ ( \text{通り} )$$
「3刻子+1順子」と「4順子②」

$$6 \times 2 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_3 = 192 \ ( \text{通り} )$$
「3刻子+1順子」と「4順子③」

$$5 \times 2 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^2 = 2,560 \ ( \text{通り} )$$
「3刻子+1順子」と「4順子④」

$${}_5 \mathrm{P}_2 \times ({}_4 \mathrm{C}_1)^3 \times ({}_4 \mathrm{C}_3)^3 = 81,920 \ ( \text{通り} )$$
$95,431 \ ( \text{通り} )$
数牌12枚の有効なパターン数は
$$32,256+656,103+4,555,416+14,705,664+20,545,775-95,431 = 40,399,783\ ( \text{通り} )$$
数牌14枚(4面子+雀頭)
4刻子+雀頭

$${}_9 \mathrm{C}_4 \times 5 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^4 = 967,680 \ ( \text{通り} )$$
3刻子+1順子+雀頭

$$7 \times [ {}_6 \mathrm{C}_3 \times \{ 3 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^3 + 3 \times ({}_4 \mathrm{C}_1)^2 \times ({}_4 \mathrm{C}_3)^4 \} + {}_6 \mathrm{C}_2 \times 3 \times \{ 4 \times ({}_4 \mathrm{C}_1)^2 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 + 2 \times {}_4 \mathrm{C}_1 \times ({}_4 \mathrm{C}_3)^3 \} + 6 \times {}_3 \mathrm{C}_2 \times \{ 5 \times {}_4 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 1 \times ({}_4 \mathrm{C}_3)^2 \} + 1 \times 6 \times {}_4 \mathrm{C}_2 ] = 14,201,628 \ ( \text{通り} )$$
2刻子+2順子+雀頭
①
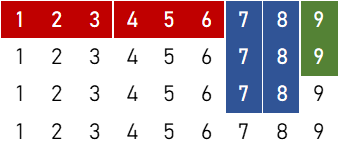
$${}_5 \mathrm{C}_2 \times [ {}_3 \mathrm{C}_2 \times \{ 1 \times ({}_4 \mathrm{C}_1)^6 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 + 6 \times ({}_4 \mathrm{C}_1)^5 \times ({}_4 \mathrm{C}_3)^3 \} + 3 \times 6 \times { 2 \times ({}_4 \mathrm{C}_1)^5 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 5 \times ({}_4 \mathrm{C}_1)^4 \times ({}_4 \mathrm{C}_3)^2 } + {}_6 \mathrm{C}_2 \times { 3 \times ({}_4 \mathrm{C}_1)^4 \times {}_4 \mathrm{C}_2 + 4 \times ({}_4 \mathrm{C}_1)^3 \times {}_4 \mathrm{C}_3 } ] = 36,971,520 \ ( \text{通り} )$$
②
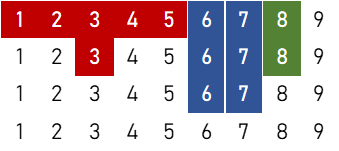
$$ = 14,595,680 \ ( \text{通り} )$$
③

$$ = 12,125,592 \ ( \text{通り} )$$
④

$$ = 8,890,560 \ ( \text{通り} )$$
$72,583,352 \ ( \text{通り} )$
1刻子+3順子+雀頭
①

$$7 \times 6 \times 5 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^4 = 322,560 \ ( \text{通り} )$$
②

$$ = 2,261,952 \ ( \text{通り} )$$
③

$$ = 7,787,520 \ ( \text{通り} )$$
④
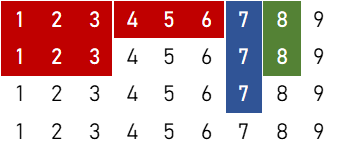
$$ = 55,676,160 \ ( \text{通り} )$$
⑤

$$ = 3,893,760 \ ( \text{通り} )$$
⑥
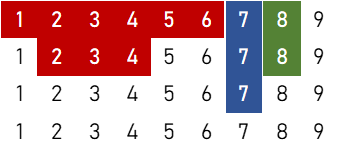
$$ = 22,270,464 \ ( \text{通り} )$$
⑦
$$ = 49,139,712 \ ( \text{通り} )$$
⑧

$$ = 12,284,928 \ ( \text{通り} )$$
⑨

$$ = 29,466,624 \ ( \text{通り} )$$
⑩

$$1 \times 9 \times 8 \times ({}_4 \mathrm{C}_1)^7 \times {}_4 \mathrm{C}_3 = 4,718,592 \ ( \text{通り} )$$
$187,822,272 \ ( \text{通り} )$
4順子+雀頭

| 番号 | 順子並び | 左右対称 | 0段 | 1段 | 2段 | 3段 | 組合せ数 |
| ① | 7 | 1 | 6 | 0 | 0 | 0 | 252 |
| ② | 6 | 2 | 5 | 1 | 0 | 1 | 5,952 |
| ③ | 5 | 2 | 4 | 2 | 0 | 2 | 66,560 |
| ④ | 20 | 1 | 3 | 3 | 0 | 3 | 1,720,320 |
| ⑤ | 6 | 1 | 5 | 0 | 2 | 0 | 6,552 |
| ⑥ | 5 | 2 | 4 | 1 | 2 | 1 | 145,920 |
| ⑦ | 4 | 2 | 3 | 2 | 2 | 2 | 1,499,136 |
| ⑧ | 12 | 1 | 2 | 4 | 1 | 2 | 4,767,744 |
| ⑨ | 5 | 1 | 4 | 0 | 4 | 0 | 159,840 |
| ⑩ | 4 | 2 | 3 | 1 | 4 | 1 | 3,262,464 |
| ⑪ | 3 | 2 | 2 | 3 | 3 | 1 | 5,142,528 |
| ⑫ | 6 | 1 | 1 | 5 | 2 | 1 | 10,027,008 |
| ⑬ | 10 | 1 | 3 | 0 | 6 | 0 | 8,864,640 |
| ⑭ | 12 | 1 | 2 | 2 | 5 | 0 | 22,146,048 |
| ⑮ | 6 | 1 | 1 | 4 | 4 | 0 | 21,233,664 |
| ⑯ | 3 | 1 | 0 | 6 | 3 | 0 | 17,252,352 |
| ⑰ | 5 | 1 | 4 | 2 | 0 | 2 | 33,280 |
| ⑱ | 4 | 2 | 3 | 3 | 0 | 3 | 688,128 |
| ⑲ | 12 | 1 | 2 | 4 | 1 | 2 | 4,767,744 |
| ⑳ | 4 | 1 | 3 | 2 | 2 | 2 | 749,568 |
| ㉑ | 3 | 2 | 2 | 3 | 3 | 1 | 5,142,528 |
| ㉒ | 6 | 1 | 1 | 5 | 2 | 1 | 10,027,008 |
| ㉓ | 3 | 1 | 2 | 2 | 5 | 0 | 5,536,512 |
| ㉔ | 2 | 2 | 1 | 4 | 4 | 0 | 14,155,776 |
| ㉕ | 1 | 2 | 0 | 6 | 3 | 0 | 11,501,568 |
| ㉖ | 3 | 1 | 1 | 4 | 4 | 0 | 10,616,832 |
| ㉗ | 2 | 1 | 0 | 6 | 3 | 0 | 11,501,568 |
| ㉘ | 3 | 1 | 2 | 4 | 1 | 2 | 1,191,936 |
| ㉙ | 6 | 1 | 1 | 5 | 2 | 1 | 10,027,008 |
| ㉚ | 2 | 1 | 1 | 4 | 4 | 0 | 7,077,888 |
| ㉛ | 1 | 2 | 0 | 6 | 3 | 0 | 11,501,568 |
| ㉜ | 1 | 1 | 0 | 6 | 3 | 0 | 5,750,784 |
| 合計 | 206,570,676 | ||||||
かぶりによる除外
$40,284,212 \ ( \text{通り} )$
数牌14枚の有効なパターン数は
$$967,680+14,201,628+72,583,352+187,822,272+206,570,676-41,551,924 = 440,593,684\ ( \text{通り} )$$
まとめ
今回は、天和の確率の補足記事として、数牌1種類での和了パターン数を枚数ごとに詳しく求めてみました。














