皆さん、麻雀ってやりますか?
昔はグレーな遊びという認識が一般的でしたが、最近では「Mリーグ」などプロによる競技麻雀の普及もあり、老若男女問わず遊べるクリーンなイメージも出てきたように思います。
私個人としては、プロフィール の趣味にも書くほど大好きです(笑)
今回は、そんな麻雀における伝説の役満「天和」の確率を、(私にとっては難解な)アルゴリズムやプログラムを使わず、手計算で計算して求めたいと思います。
「天和」とは?
「天和」とは、麻雀における「役」の1つです。
親の配牌の時点で和了形になっている役のことで、トップクラスで出現確率の低い役満として有名です。
配牌の時点で決まるので、狙って出せる役ではありません。
麻雀プロの生放送対局で初めて「天和」が出たときの映像です。
月島ひかるプロ、めちゃくちゃ喜んでます(笑)
この一瞬で16000オール、子は笑うしかありません。
前提条件・計算の方針
- 使用する牌は、数牌108枚(萬子・筒子・索子の1~9/各4枚)と字牌28枚(東・南・西・北・白・發・中/各4枚)を合わせた、計34種136枚とします。
- 計算に影響する牌(花牌・白ポッチなど)は考慮しません。
- 和了の形式は、4面子+雀頭・七対子・国士無双とします。
ただし、同一牌を4枚使った七対子は無効とします。 - 「136枚の中から無作為に14枚を選んだとき、それが和了形である確率」を求めます。
- 「全体のパターン数(14枚の選び方の総数)」を求めます(これは簡単です)。
- 「和了形となるパターン数」を求めます(これが激ムズです)。
- 「和了形となるパターン数」を「全体のパターン数」で除して、天和の確率を求めます。
いざ、計算!
全体のパターン数
136枚の中から14枚を選ぶパターン数は ${}_{136} \mathrm{C}_{14}$ 通りです。
具体的に計算すると
$${}_{136} \mathrm{C}_{14} = 4,250,305,029,168,216,000 \ ( \text{通り} )$$となり、約425京通りです。
${}_n \mathrm{C}_r$ とは、「異なる $n$ 個の中から $r$ 個を選ぶパターン数」を表し
$$ {}_n \mathrm{C}_r = \dfrac{n!}{r!(n-r)!} = \dfrac{ \overbrace{ n(n-1)(n-2) \cdots (n-r+1) }^{ r \text{ 個の積 } } }{ \underbrace{ r(r-1)(r-2) \cdots 3 \cdot 2 \cdot 1 }_{ r \text{ 個の積 } } } $$により計算します。
例えば、![]()
![]()
![]()
![]()
![]() という異なる5枚の牌から2枚を選ぶパターン数は
という異なる5枚の牌から2枚を選ぶパターン数は
$${}_5 \mathrm{C}_2 = \dfrac{5 \cdot 4}{2 \cdot 1} = 10 \ ( \text{通り} )$$ だと分かります。
実際に数え上げてみると、
①![]()
![]() ②
②![]()
![]() ③
③![]()
![]() ④
④![]()
![]() ⑤
⑤![]()
![]() ⑥
⑥![]()
![]() ⑦
⑦![]()
![]() ⑧
⑧![]()
![]() ⑨
⑨![]()
![]() ⑩
⑩![]()
![]()
となり、確かに10通りであることが確認できます。
また一般に、「異なる $n$ 個の中から $r$ 個を選ぶパターン数」は裏を返せば「異なる $n$ 個の中から“選ばない $(n-r)$ 個”を決めるパターン数」と同じなので
$${}_n \mathrm{C}_r = {}_n \mathrm{C}_{n-r}$$ が成り立ちます。(例:${}_7 \mathrm{C}_5 = {}_7 \mathrm{C}_2 = 21$ )
和了形となるパターン数
国士無双
国士無双のパターン数は
$$13 \times {}_4 \mathrm{C}_2 \times 4^{12} = 1,308,622,848 \ ( \text{通り} )$$
七対子
7組の対子(すべて異なる対子とする。)のパターン数は
$${}_{34} \mathrm{ C }_7 \times ( {}_4 \mathrm{C}_2 )^7 = 1,505,948,184,576 \ ( \text{通り} )$$
この中には、「二盃口」の形も含まれています。(例:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)
「二盃口」は後ほど「4面子+雀頭」のところでカウントするので、ここで省いておきます。
二盃口を含む七対子のパターン数は
雀頭以外の12枚が1種類で構成されているとき
(例:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)
$$\begin{eqnarray}
{}_3 \mathrm{C}_1 \times \{ (34 \ – \ 6) + 6 \times (34 \ – \ 7) + 3 \times (34 \ – \ 8) \} \times ( {}_4 \mathrm{C}_2 )^7 \\
= 225,068,544 \ ( \text{通り} )
\end{eqnarray}$$
雀頭以外の12枚が2種類で構成されているとき
(例:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)
$$\begin{eqnarray}
{}_3 \mathrm{C}_2 \times [ \{ (34 \ – \ 6) + 6 \times (34 \ – \ 7) \} \\
+ 6 \times \{ (34 \ – \ 7) + 6 \times (34 \ – \ 8) \} ] \times ( {}_4 \mathrm{C}_2 )^7 \\
= 1,081,672,704 \ ( \text{通り} )
\end{eqnarray}$$
よって、七対子(二盃口を含まない)のパターン数は
$$\begin{eqnarray}
1,505,948,184,576 \ – \ ( 225,068,544 + 1081,672,704 ) \\
= 1,504,641,443,328 \ ( \text{通り} )
\end{eqnarray}$$
4面子+雀頭
この和了形において、14枚のうち字牌・萬子・筒子・索子の数を数えると、0枚、2枚、3枚、5枚、6枚、8枚、9枚、11枚、12枚、14枚のいずれかとなります。
1面子は3枚、雀頭は2枚なので、ある1種類に注目するとその枚数は $3n$ (枚)もしくは $3n+2$ (枚)( $n=0,1,2,3,4$ )となります。
1枚、4枚、7枚、10枚、13枚はこの形で表せないので、ある1種類の枚数にはなりえません。
字牌と数牌は、それぞれの枚数さえ決まれば、そのパターン数は互いに影響を及ぼしません。
例えば、字牌5枚・索子9枚からなる和了形のパターン数は、「字牌5枚の(有効な)パターン数」と「数牌9枚の(有効な)パターン数」の積により簡単に求められます。
よって、まずは字牌・数牌のそれぞれにおいて、0枚、2枚、3枚、5枚、6枚、8枚、9枚、11枚、12枚、14枚それぞれの有効なパターン数を求めていきます。
0枚
「字牌が1枚もない」という $1$ 通りです。
2枚(雀頭)
$$7 \times {}_4 \mathrm{C}_2 = 42 \ ( \text{通り} )$$
3枚(1面子)
$$7 \times {}_4 \mathrm{C}_3 = 28 \ ( \text{通り} )$$
5枚(1面子+雀頭)
$${}_7 \mathrm{P}_2 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 = 1,008 \ ( \text{通り} )$$
6枚(2面子)
$${}_7 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 336 \ ( \text{通り} )$$
8枚(2面子+雀頭)
$${}_7 \mathrm{C}_2 \times 5 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 10,080 \ ( \text{通り} )$$
9枚(3面子)
$${}_7 \mathrm{C}_3 \times ( {}_4 \mathrm{C}_3 )^3 = 2,240 \ ( \text{通り} )$$
11枚(3面子+雀頭)
$${}_7 \mathrm{C}_3 \times 4 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^3 = 53,760 \ ( \text{通り} )$$
12枚(4面子)
$${}_7 \mathrm{C}_4 \times ( {}_4 \mathrm{C}_3 )^4 = 8,960 \ ( \text{通り} )$$
14枚(4面子+雀頭)
$${}_7 \mathrm{C}_4 \times 3 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^4 = 161,280 \ ( \text{通り} )$$
0枚
「数牌が1枚もない」という $1$ 通りです。
2枚(雀頭)
$$9 \times {}_4 \mathrm{C}_2 = 54 \ ( \text{通り} )$$
3枚(1面子)
$$9 \times {}_4 \mathrm{C}_3 + 7 \times 4^3 = 484 \ ( \text{通り} )$$
5枚(1面子+雀頭)
$$\begin{eqnarray}
{}_9 \mathrm{P}_8 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 7 \times ( 6 \times 4^3 \times {}_4 \mathrm{C}_2 + 3 \times 4^2 \times {}_4 \mathrm{C}_3 ) \\
= 19,200 \ ( \text{通り} )
\end{eqnarray}$$
6枚(2面子)
ーうち「刻子×2」
$${}_9 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 576 \ ( \text{通り} )$$
ーうち「刻子+順子」
$$7 \times (3 \times 4^2 + 6 \times 4^3 \times {}_4 \mathrm{C}_3) = 11,088 \ ( \text{通り} )$$
ーうち「順子×2」
$$\begin{eqnarray}
7 \times ( {}_4 \mathrm{C}_2 )^3 + 6 \times 4^2 \times ( {}_4 \mathrm{C}_2 )^2 + 5 \times 4^4 \times {}_4 \mathrm{C}_2 + 10 \times 4^6 \\
= 53,608 \ ( \text{通り} )
\end{eqnarray}$$
$$576+11,088+53,608 = 65,272 \ ( \text{通り} )$$
8枚(2面子+雀頭)
ーうち「刻子×2」
$${}_9 \mathrm{C}_2 \times 7 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 = 24,192 \ ( \text{通り} )$$
ーうち「刻子+順子」
$$\begin{eqnarray}
7 \times \{ {}_6 \mathrm{P}_2 \times 4^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 3 \times 2 \times 4 \times {}_4 \mathrm{C}_3 \\
+ 3 \times 6 \times 4^2 \times {}_4 \mathrm{C}_2 + 3 \times 6 \times 4^2 \times ( {}_4 \mathrm{C}_3 )^2 \} \\
– \ 6 \times 4^2 \times ( {}_4 \mathrm{C}_3 )^2 \\
= 366,048 \ ( \text{通り} )
\end{eqnarray}$$
ーうち「順子×2」
$$\begin{eqnarray}
{}_5 \mathrm{C}_2 \times (3 \times 4^6 \times {}_4 \mathrm{C}_2 + 6 \times 4^5 \times {}_4 \mathrm{C}_3 ) \\
+ 7 \times \{ 6 \times ({}_4 \mathrm{C}_2)^4 + 3 \times ({}_4 \mathrm{C}_2)^2 \} \ – \ 6 \times ({}_4 \mathrm{C}_2)^4 \\
+ 5 \times \{ 4 \times 4^4 \times ({}_4 \mathrm{C}_2)^2 + 4 \times 4^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 +4^4 \} \\
+ 6 \times \{ 5 \times 4^2 \times ({}_4 \mathrm{C}_2)^3 + 2 \times 4 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 \\
+ 2 \times 4^2 \times {}_4 \mathrm{C}_2 \} = 1,358,516 \ ( \text{通り} )
\end{eqnarray}$$
$$24,192+366,048+1,358,516 = 1,748,756 \ ( \text{通り} )$$
9枚(3面子)
ーうち「刻子×3」
$${}_9 \mathrm{C}_3 \times ({}_4 \mathrm{C}_3)^3 = 5,376 \ ( \text{通り} )$$
ーうち「刻子×2+順子×1」
$$\begin{eqnarray}
7 \times \{ {}_6 \mathrm{C}_2 \times 4^3 \times ({}_4 \mathrm{C}_3)^2 + 6 \times 3 \times 4^2 \times {}_4 \mathrm{C}_3 + {}_3 \mathrm{C}_2 \times 4 \} \\
= 115,668 \ ( \text{通り} )
\end{eqnarray}$$
ーうち「刻子×1+順子×2」
$$\begin{eqnarray}
{}_5 \mathrm{C}_2 \times (3 \times 4^6 \times {}_4 \mathrm{C}_3 + 6 \times 4^5) \\
+ 5 \times (4 \times 4^4 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + 4 \times 4^3 \times {}_4 \mathrm{C}_2) \\
+ 6 \times \{ 5 \times 4^2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 2 \times 4 \times ({}_4 \mathrm{C}_2)^2 \} \\
+ 7 \times 6 \times ({}_4 \mathrm{C}_2)^3 \times {}_4 \mathrm{C}_3 \\
= 790,656 \ ( \text{通り} )
\end{eqnarray}$$
ーうち「順子×3」
$$\begin{eqnarray}
4^9 + 3 \times 4^5 \times ({}_4 \mathrm{C}_2)^2 + 4 \times 2 \times 4^3 \times ({}_4 \mathrm{C}_2)^3 \\
+ 5 \times 3 \times 4^2 \times ({}_4 \mathrm{C}_2)^2 \times {}_4 \mathrm{C}_3 + 6 \times 2 \times 4 \times {}_4 \mathrm{C}_2 \times ({}_4 \mathrm{C}_3)^2 \\
+ 3 \times 2 \times 4^7 \times {}_4 \mathrm{C}_2 + 4 \times 3 \times 4^5 \times ({}_4 \mathrm{C}_2)^2 + 5 \times 4 \times 4^3 \times ({}_4 \mathrm{C}_2)^3 \\
= 1,831,168 \ ( \text{通り} )
\end{eqnarray}$$
$$\begin{eqnarray}
5,376+115,668+790,656+1,831,168 \\
= 2,742,868 \ ( \text{通り} )
\end{eqnarray}$$
11枚(3面子+雀頭)
ーうち「刻子×3」
$${}_9 \mathrm{C}_3 \times 6 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^3 = 193,536 \ ( \text{通り} )$$
ーうち「刻子×2+順子×1」
$$ = 3,132,708 \ ( \text{通り} )$$
ーうち「刻子×1+順子×2」
$$ = 15,759,008 \ ( \text{通り} )$$
ーうち「順子×3」
$$ = 27,952,128 \ ( \text{通り} )$$
$$\begin{eqnarray}
193,536+3,132,708+15,759,008+27,952,128 \\
= 47,037,380 \ ( \text{通り} )
\end{eqnarray}$$
12枚(4面子)
ーうち「刻子×4」
$${}_9 \mathrm{C}_4 \times ({}_4 \mathrm{C}_3)^4 = 32,256 \ ( \text{通り} )$$
ーうち「刻子×3+順子×1」
$$\begin{eqnarray}
7 \times \{ {}_6 \mathrm{C}_3 \times 4^3 \times ({}_4 \mathrm{C}_3)^3 + {}_6 \mathrm{C}_2 \times 3 \times 4^2 \times ( {}_4 \mathrm{C}_3 )^2 \\
+ 6 \times 3 \times 4 \times {}_4 \mathrm{C}_3 + 1 \} = 656,103 \ ( \text{通り} )
\end{eqnarray}$$
ーうち「刻子×2+順子×2」
$$\begin{eqnarray}
{}_5 \mathrm{C}_2 \times \{ {}_3 \mathrm{C}_2 \times 4^6 \times ( {}_4 \mathrm{C}_3 )^2 + 3 \times 6 \times 4^5 \times {}_4 \mathrm{C}_3 + {}_6 \mathrm{C}_2 \times 4^4 \} \\
+ 5 \times \{ {}_4 \mathrm{C}_2 \times 4^4 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^2 + 4 \times 4 \times 4^3 \times {}_4 \mathrm{C}_2 \times {}_4 \mathrm{C}_3 + {}_4 \mathrm{C}_2 \times 4^2 \times {}_4 \mathrm{C}_2 \} \\
+ 6 \times { {}_5 \mathrm{C}_2 \times 4^2 \times ( {}_4 \mathrm{C}_2 )^2 \times ( {}_4 \mathrm{C}_3 )^2 + 5 \times 2 \times 4 \times ( {}_4 \mathrm{C}_2 )^2 \times {}_4 \mathrm{C}_3 + ( {}_4 \mathrm{C}_2 )^2 } \\
+ 7 \times {}_6 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_2 )^3 \times ( {}_4 \mathrm{C}_3 )^2 \\
= 4,555,416 \ ( \text{通り} )
\end{eqnarray}$$
ーうち「刻子×1+順子×3」
$$ = 14,694,912 \ ( \text{通り} )$$
ーうち「順子×4」
$$ = 20,461,096 \ ( \text{通り} )$$
$$\begin{eqnarray}
32,256+656,103+4,555,416+14,694,912+20,461,096 \\
= 40,399,783 \ ( \text{通り} )
\end{eqnarray}$$
14枚(4面子+雀頭)
ーうち「刻子×4」
$${}_9 \mathrm{C}_4 \times 5 \times {}_4 \mathrm{C}_2 \times ( {}_4 \mathrm{C}_3 )^3 = 967,680 \ ( \text{通り} )$$
ーうち「刻子×3+順子×1」
$$ = 13,940,412 \ ( \text{通り} )$$
ーうち「刻子×2+順子×2」
$$ = 68,873,784 \ ( \text{通り} )$$
ーうち「刻子×1+順子×3」
$$ = 172,904,224 \ ( \text{通り} )$$
ーうち「順子×4」
$$ = 183,907,584 \ ( \text{通り} )$$
$$\begin{eqnarray}
967,680 + 13,940,412 + 68,873,784 \\
+ 172,904,224 + 183,907,584 \\
= 440,593,684 \ ( \text{通り} )
\end{eqnarray}$$
上で求めた「有効なパターン数」を、見やすいように表にまとめておきます。
| 字牌 | 数牌 | |
| 0枚 | 1 | 1 |
| 2枚 | 42 | 54 |
| 3枚 | 28 | 484 |
| 5枚 | 1,008 | 19,200 |
| 6枚 | 336 | 65,272 |
| 8枚 | 10,080 | 1,748,756 |
| 9枚 | 2,240 | 2,742,868 |
| 11枚 | 53,760 | 47,037,380 |
| 12枚 | 8,960 | 40,399,783 |
| 14枚 | 161,280 | 440,593,684 |
字牌は雀頭か刻子しか作れないのに対し、数牌は雀頭・刻子に加え順子も作れるので、パターン数も大きく変わってきますね。
上で求めた「有効なパターン数」を用いて、14枚を構成する字牌と数牌の構成枚数ごとのパターン数を求めていきます。
字牌14枚+数牌0枚
必ず字一色となりますね。
$$\underbrace{ 161,280 }_{ \text{字牌14枚} } \times \underbrace{ 1 }_{ \text{数牌0枚} } = 161,280 \ ( \text{通り} )$$
字牌12枚+数牌2枚
「数牌2枚」は「雀頭」ですので、必ず1種類となります。
$$\underbrace{ 8,960 }_{ \text{字牌12枚} } \times \underbrace{ 54 \times 3 }_{ \text{数牌2枚} } = 1,451,520 \ ( \text{通り} )$$
字牌11枚+数牌3枚
「数牌3枚」は「1面子」ですので、必ず1種類となります。
$$\underbrace{ 53,760 }_{ \text{字牌11枚} } \times \underbrace{ 484 \times 3 }_{ \text{数牌3枚} } = 78,059,520 \ ( \text{通り} )$$
字牌9枚+数牌5枚
「数牌5枚」は「1面子+雀頭」であり、以下の2パターンが考えられます。
- 1種類で5枚(例:




 )
) - 2種類で3枚+2枚(例:




 )
)
$$\begin{eqnarray}
\underbrace{ 2,240 }_{ \text{字牌9枚} } \times ( \underbrace{ 19,200 \times 3 }_{ \text{Ⓐ5枚} } + \underbrace{ 484 \times 54 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ3枚+Ⓑ2枚} } ) \\[0.5em]
= 480,291,840 \ ( \text{通り} )
\end{eqnarray}$$
字牌8枚+数牌6枚
「数牌6枚」は「2面子」であり、以下の2パターンが考えられます。
- 1種類で6枚(例:





 )
) - 2種類で3枚+3枚(例:





 )
)
$$\begin{eqnarray}
\underbrace{ 10,080 }_{ \text{字牌8枚} } \times ( \underbrace{ 65,272 \times 3 }_{ \text{Ⓐ6枚} } + \underbrace{ 484^2 \times {}_3 \mathrm{C}_2 }_{ \text{Ⓐ3枚+Ⓑ3枚} } ) \\[0.5em]
= 9,057,726,720 \ ( \text{通り} )
\end{eqnarray}$$
字牌6枚+数牌8枚
「数牌8枚」は「2面子+雀頭」であり、以下の4パターンが考えられます。
- 1種類で8枚
(例:






 )
) - 2種類で6枚+2枚
(例:






 )
) - 2種類で5枚+3枚
(例:






 )
) - 3種類で3枚+3枚+2枚
(例:






 )
)
$$\begin{eqnarray}
\underbrace{ 336 }_{ \text{字牌6枚} } \times ( \underbrace{ 1,748,756 \times 3 }_{ \text{Ⓐ8枚} } + \underbrace{ 65,272 \times 54 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ6枚+Ⓑ2枚} } \\
+ \underbrace{ 19,200 \times 484 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ5枚+Ⓑ3枚} } + \underbrace{ 484^2 \times 54 \times 3 }_{ \text{Ⓐ3枚+Ⓑ3枚+Ⓒ2枚} } ) \\[0.5em]
= 40,353,824,448 \ ( \text{通り} )
\end{eqnarray}$$
字牌5枚+数牌9枚
「数牌9枚」は「3面子」であり、以下の3パターンが考えられます。
- 1種類で9枚
(例:






 )
) - 2種類で6枚+3枚
(例:







 )
) - 3種類で3枚+3枚+3枚
(例:






 )
)
$$\begin{eqnarray}
\underbrace{ 1,008 }_{ \text{字牌5枚} } \times ( \underbrace{ 2,742,868 \times 3 }_{\text{Ⓐ9枚}} + \underbrace{ 65,272 \times 484 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ6枚+Ⓑ3枚} } + \underbrace{ 484^3 }_{ \text{Ⓐ3枚+Ⓑ3枚+Ⓒ3枚} } ) \\[0.5em]
= 313,647,663,168 \ ( \text{通り} )
\end{eqnarray}$$
字牌3枚+数牌11枚
「数牌11枚」は「3面子+雀頭」であり、以下の6パターンが考えられます。
- 1種類で11枚
(例:








 )
) - 2種類で9枚+2枚
(例:








 )
) - 2種類で8枚+3枚
(例:









 )
) - 2種類で6枚+5枚
(例:









 )
) - 3種類で6枚+3枚+2枚
(例:









 )
) - 3種類で5枚+3枚+3枚
(例:








 )
)
$$\begin{eqnarray}
\underbrace{ 28 }_{ \text{字牌3枚} } \times ( \underbrace{ 47,037,380 \times 3 }_{ \text{Ⓐ11枚} } + \underbrace{ 2,742,868 \times 54 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ9枚+Ⓑ2枚} } \\
+ \underbrace{ 1,748,756 \times 484 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ8枚+Ⓑ3枚} } + \underbrace{ 65,272 \times 19,200 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ6枚+Ⓑ5枚} } \\
+ \underbrace{ 65,272 \times 484 \times 54 \times 3! }_{ \text{Ⓐ6枚+Ⓑ3枚+Ⓒ2枚} } + \underbrace{ 19,200 \times 484^2 \times 3 }_{ \text{Ⓐ5枚+Ⓑ3枚+Ⓒ3枚} } ) \\[0.5em]
= 1,045,978,156,944 \ ( \text{通り} )
\end{eqnarray}$$
字牌2枚+数牌12枚
「数牌12枚」は「4面子」であり、以下の4パターンが考えられます。
- 1種類で12枚
(例:









 )
) - 2種類で9枚+3枚
(例:









 )
) - 2種類で6枚+6枚
(例:










 )
) - 3種類で6枚+3枚+3枚
(例:









 )
)
$$\begin{eqnarray}
\underbrace{ 42 }_{ \text{字牌2枚} } \times ( \underbrace{ 40399783 \times 3 }_{ \text{Ⓐ12枚} } + \underbrace{ 2,742,868 \times 484 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ9枚+Ⓑ3枚} } \\
+ \underbrace{ 65,272^2 \times {}_3 \mathrm{C}_2 }_{ \text{Ⓐ6枚+Ⓑ6枚} } + \underbrace{ 65,272 \times 484^2 \times 3 }_{ \text{Ⓐ6枚+Ⓑ3枚+Ⓒ3枚} } ) \\[0.5em]
= 2,803,032,240,498 \ ( \text{通り} )
\end{eqnarray}$$
字牌0枚+数牌14枚
「数牌14枚」は「4面子+雀頭」であり、以下の9パターンが考えられます。
- 1種類で14枚
(例:











 )
) - 2種類で12枚+2枚
(例:











 )
) - 2種類で11枚+3枚
(例:











 )
) - 2種類で9枚+5枚
(例:











 )
) - 2種類で8枚+6枚
(例:












 )
) - 3種類で9枚+3枚+2枚
(例:











 )
) - 3種類で8枚+3枚+3枚
(例:











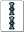
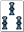 )
) - 3種類で6枚+6枚+2枚
(例:












 )
) - 3種類で6枚+5枚+3枚
(例:











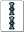
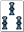 )
)
$$\begin{eqnarray}
\underbrace{ 1 }_{ \text{字牌0枚} } \times ( \underbrace{ 440,593,684 \times 3 }_{ \text{Ⓐ14枚} } + \underbrace{ 40,399,783 \times 54 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ12枚+Ⓑ2枚} } \\
+ \underbrace{ 47,037,380 \times 484 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ11枚+Ⓑ3枚} } + \underbrace{ 2,742,868 \times 19,200 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ9枚+Ⓑ5枚} } \\
+ \underbrace{ 1,748,756 \times 65,272 \times {}_3 \mathrm{P}_2 }_{ \text{Ⓐ8枚+Ⓑ6枚} } + \underbrace{ 2742868 \times 484 \times 54 \times 3! }_{ \text{Ⓐ9枚+Ⓑ3枚+Ⓒ2枚} } \\
+ \underbrace{ 1,748,756 \times 484^2 \times 3 }_{ \text{Ⓐ8枚+Ⓑ3枚+Ⓒ3枚} } + \underbrace{ 65,272^2 \times 54 \times 3 }_{ \text{Ⓐ6枚+Ⓑ6枚+Ⓒ2枚} } \\
+ \underbrace{ 65,272 \times 19,200 \times 484 \times 3! }_{ \text{Ⓐ6枚+Ⓑ5枚+Ⓒ3枚} } ) \\[0.5em]
= 7,140,498,565,560 \ ( \text{通り} )
\end{eqnarray}$$
上で求めた「構成枚数ごとのパターン数」を、見やすいように表にまとめておきます。
| 字牌 | 数牌 | パターン数 |
| 14枚 | 0枚 | 161,280 |
| 12枚 | 2枚 | 1,451,520 |
| 11枚 | 3枚 | 78,059,520 |
| 9枚 | 5枚 | 480,291,840 |
| 8枚 | 6枚 | 9,057,726,720 |
| 6枚 | 8枚 | 40,353,824,448 |
| 5枚 | 9枚 | 313,647,663,168 |
| 3枚 | 11枚 | 1,045,978,156,944 |
| 2枚 | 12枚 | 2,803,032,240,498 |
| 0枚 | 14枚 | 7,140,498,565,560 |
| 合計 | 11,353,128,141,498 | |
すべての組み合わせを合計すると、4面子+雀頭のパターン数は
$$11,353,128,141,498 \ \text{(通り)}$$ だと分かります。
和了形となるパターン数
上で求めた国士無双・七対子(二盃口を含まない)・雀頭+4面子のパターン数を足して、「和了形となるパターン数」を求めると
$$\begin{eqnarray}
1,308,622,848+1,504,641,443,328+11,353,128,141,498 \\
= 12,859,078,207,674 \ ( \text{通り} )
\end{eqnarray}$$
となり、約12兆通りです。
天和の確率
「全体のパターン数」と「和了形となるパターン数」が分かったので、ようやく天和の確率を求めることができます!
「和了形となるパターン数」を「全体のパターン数」で除すと
$$\dfrac{12,859,078,207,674}{4,250,305,029,168,216,000} = 0.0000030254483 \cdots $$
となり、天和の確率は約0.0003%(約33万0530分の1)であることが分かりました!
まとめ
今回は、麻雀の伝説役「天和」の確率を手計算で求めてみました。
約0.0003%(約33万分の1)と、非常に低い確率であることがわかりましたが、人生で1回はアガってみたいものですね~。
また、今回は手計算により計算を進めましたが、アルゴリズムやプログラムを用いた方が何倍も効率的かつ正確です。
その方法につきましては、他の方がいくつか記事を書いておられますので、そちらを参考にしてみてください。
私もプログラミングによる計算を勉強して、他人に伝えられる程度まで理解したら、記事にしようかなと思います。
お礼
本記事の執筆にあたっては、麻雀の数学|らすかるの家(らすかる様)を参考にさせていただきました。
ありがとうございます。













